Expectation
Out of 4000 families with 5 children each, how many families would you expect to have at least 1 boy?
Note: Assume that the probability of a male birth is 2 1 .
The answer is 3875.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
We could also calculate the complement, i.e., the number of families with no boys, and then subtract this value from 4000. The probability of there being no boys is ( 1 / 2 ) 5 = 1 / 3 2 , which represents ( 1 / 3 2 ) × 4 0 0 0 = 1 2 5 families, and thus we would expect there to be 4 0 0 0 − 1 2 5 = 3 8 7 5 families with at least one boy.
Log in to reply
You should put that in as a solution so that others can see it more easily. (That's how I did it too)
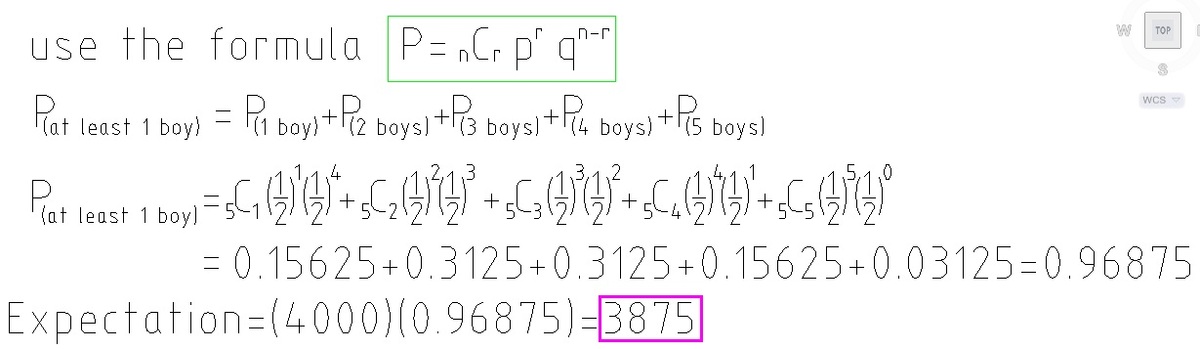
The probability that a family has at least one boy is the complement of the probability that a family includes no boys. The probability that a family has no boys is ( 1 / 2 ) 5 = 1 / 3 2 , so the probability that a family has at least one boy is 1 − ( 1 / 3 2 ) = 3 1 / 3 2 , and so out of 4 0 0 0 families we would expect ( 3 1 / 3 2 ) × 4 0 0 0 = 3 8 7 5 families to have at least one boy.