Expected Area Problem
Two toothpicks of length 1 are simultaneously dropped onto a plane. Both their positions and orientations are completely random and independent. When they intersect, they form a quadrilateral with the toothpicks as diagonals.
Given that the toothpicks intersect, what is the expected area of this quadrilateral?
The answer is 0.392699.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I have reposted Pedro Cardoso's solution here, copied from his comment to Albert Lau's solution
Given that θ is the angle between the sticks, and that they intersect, the area of the quadrilateral formed is 2 s i n ( θ ) .
Now, to find the probability that, given that the toothpicks intersect, the intersection angle is theta, consider the toothpicks as two line segments, A B and C D . say A B is fixed on the plane at, say, A = ( 0 , 0 ) and B = ( 0 , 1 ) , and call M the intersection between A B and C D , and make θ = A M D . Then, imagine moving the point C arround, moving D in the same direction fix θ constant: What is the region C can be at so that θ is fixed and C D still intersects A B ? That region is a rhombus, of its angles is θ , and its sides all measure 1 . Thus, it's area is s i n ( θ ) .
Finally, the probability that, given that the toothpicks intersect, the angle between them is θ is directly proportional to the area of that region, s i n ( θ ) (To see this intuitively, consider that there are a lot more ways to make the toothpick intersect when the angle between them is, say 4 6 º compared to when its 5 º , because, in the former, there are a lot more places C can be in that keep the toothpicks intersecting). So the probability is the weighted average of 2 s i n ( θ ) , where each area is weighted by s i n ( θ ) , namely, the probability that that area occurs (or at least, something directly proportional to this probability).
This gives us ∫ 0 π sin x d x ∫ 0 π ( 2 sin x ) sin x d x = 0 . 3 9 2 6 . . .
Mendrin: (Some) Monte Carlo simulations support this figure of 0.3926.
If the toothpicks intersect, their position dont matter, only their length and orientation. Proof :
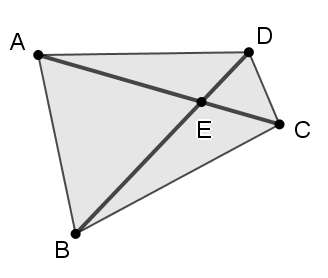
let θ be the acute angle between A C , B D S A B C D = S Δ A E B + S Δ B E C + S Δ C E D + S Δ D E A = 2 1 A E ⋅ B E sin θ + 2 1 B E ⋅ C E sin ( π − θ ) + 2 1 C E ⋅ D E sin θ + 2 1 D E ⋅ A E sin ( π − θ ) = 2 1 A E ⋅ B E sin θ + 2 1 B E ⋅ C E sin θ + 2 1 C E ⋅ D E sin θ + 2 1 D E ⋅ A E sin θ ( sin θ ≡ sin ( π − θ ) ) = 2 1 ( A E ⋅ B E + B E ⋅ C E + C E ⋅ D E + D E ⋅ A E ) sin θ = 2 1 ( A E + C E ) ⋅ ( B E + D E ) sin θ = 2 1 A C ⋅ B D sin θ
Back to the problem, A C = B D = 1 , area = 2 1 sin θ
<edit: the solution hereafter is incorrect, please check other solution>
Consider the average value of 2 1 sin θ , 0 ≤ θ ≤ 2 π
expected area = ∫ 0 π / 2 2 1 sin θ d θ ÷ 2 π = π 1 = 0 . 3 1 8 3
However, shouldn't the toothpicks' orientation also affect the probability they intersect? (Like the probability two toothpicks intersect at 90° is larger than that of 10°)
Log in to reply
yes u're right. this question has some problem and the solution is incorrect, please make a report.
The problem states they intersect. (Maybe it was changed.) I agree with your solution.
Almost correct! Should it not be integral{0.5(x)(sinx)dx} same bounds? Dividing by pi/2 does not make sense to me
Log in to reply
consider the average value of (sin x)^2 from x=0~10000pi , since 0 < (sin x)^2 < 1, dont u think the average is between 0~1? integrate over 0~10000pi instead u will get a humongous number. thats because the value represent "sum", dividing 10000pi turn the "sum" into "average".
same case for 0~pi/2 here. the result is still incorrect tho, see report for more info.
Here is my solution:
Given that θ is the angle between the sticks, and that they intersect, the area of the quadrilateral formed is 2 s i n ( θ ) .
Now, to find the probability that, given that the toothpicks intersect, the intersection angle is theta, consider the toothpicks as two line segments, A B and C D . say A B is fixed on the plane at, say, A = ( 0 , 0 ) and B = ( 0 , 1 ) , and call M the intersection between A B and C D , and make θ = A M D . Then, imagine moving the point C arround, moving D in the same direction fix θ constant: What is the region C can be at so that θ is fixed and C D still intersects A B ? That region is a rhombus, of its angles is θ , and its sides all measure 1 . Thus, it's area is s i n ( θ ) .
Finally, the probability that, given that the toothpicks intersect, the angle between them is θ is directly proportional to the area of that region, s i n ( θ ) (To see this intuitively, consider that there are a lot more ways to make the toothpick intersect when the angle between them is, say 4 6 º compared to when its 5 º , because, in the former, there are a lot more places C can be in that keep the toothpicks intersecting). So the probability is the weighted average of 2 s i n ( θ ) , where each area is weighted by s i n ( θ ) , namely, the probability that that area occurs (or at least, something directly proportional to this probability).
This gives us ∫ 0 π sin x d x ∫ 0 π ( 2 sin x ) sin x d x = 0 . 3 9 2 6 . . .
I did the same, 1/π .. :'(
We can find the area of the quadrilateral by considering the quadrilateral as two triangles stuck together. If the angle between two toothpicks is θ , the triangles will have base 1, and heights a and b where a + b = sin ( θ ) . The area will be 2 a + 2 b = 2 sin ( θ ) . We need to notice that if two randomly dropped toothpicks happen to intersect, it is more likely that the angle between them will be near perpendicular, than near parallel. Taking this into account, the expected area will be ∫ 0 2 π 2 sin ( θ ) p ( θ ) where p ( θ ) is the proabability that two randomly dropped intersecting toothpicks, intersect at θ . WLOG, we can say that the first toothpick dropped is vertical. The probability that a second randomly dropped toothpick will intersect the first, will be proportional to the horizontal span of the second toothpick (which equals sin ( θ ) ). Therefore, the probability two randomly dropped intersecting toothpicks, intersect at θ is ∫ 0 2 π sin ( θ ) d θ sin ( θ ) d θ = sin ( θ ) d θ Therefore the expected area of the quadrilateral will be 2 1 ∫ 0 2 π sin 2 ( θ ) d θ = 8 π ≈ 0 . 3 9 2 7 The answer that Brilliant wants is not correct. That answer comes from assuming that p ( θ ) is constant, which is not true. If we randomly drop two toothpicks onto the plane and they happen to intersect, it will be more likely that they are near perpendicular than near parallel. We can't assume that all values of θ are equally likely. <edit: This problem has been updated to accept the correct answer>
Moderator note : The correct answer has since been updated.