Expected value and recursion lll
A toad is placed in a 5x5 square. It jumps to an adjacent square or the square next to adjacent square (i.e. the square within 1 square from current square)all with equal probability. There are traps on the corner squares , when toad is placed on one of these traps it dies immediately.
The toad is randomly placed in a square.
If it is alive it will keep jumping till it dies
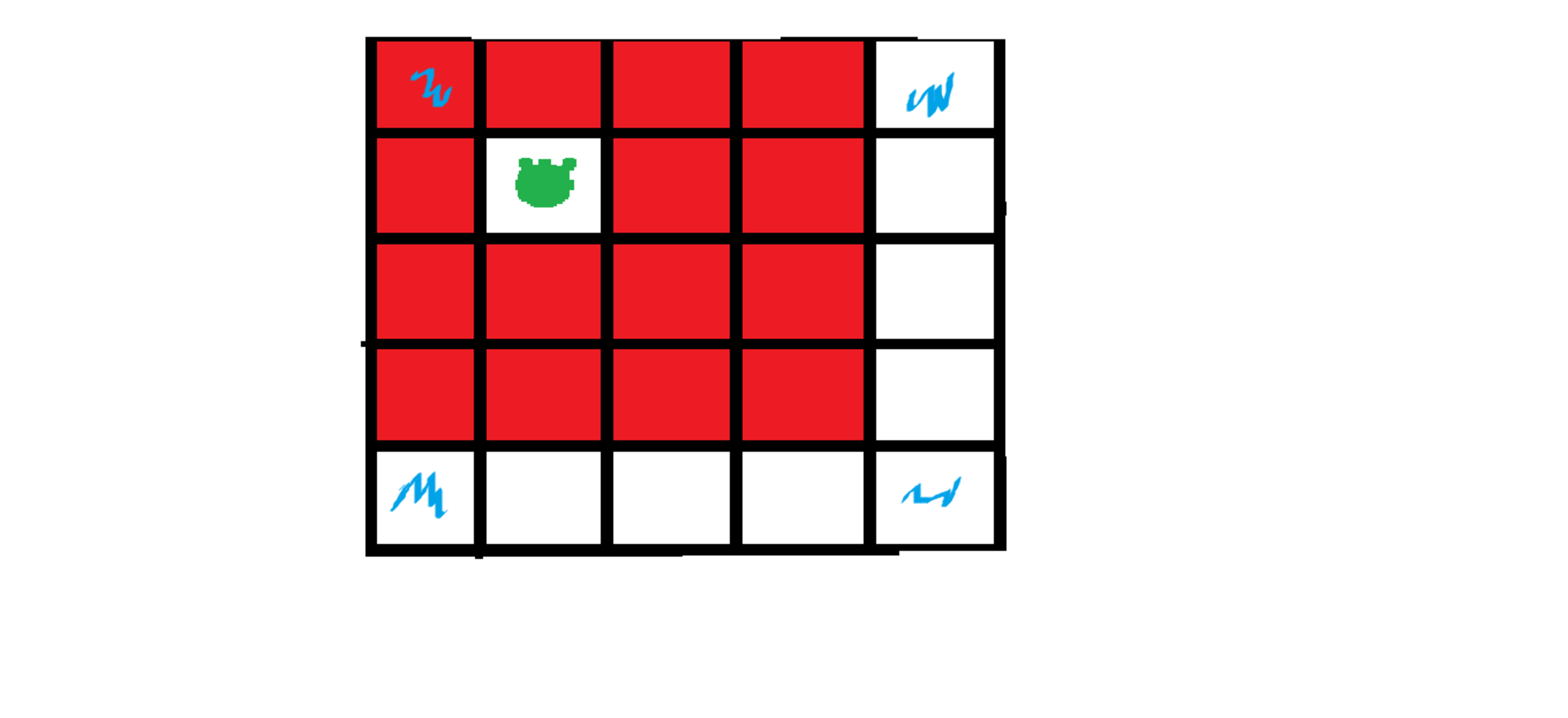
In the picture traps are displayed in blue color and possible choices are represented by Red. Toad is green. What is expected number of jumps taken by frog till it dies. If answer is in fraction , submit numerator + denominator.
You will need wolfram alpha. Suggested quiz : Linearity of expectations.
The answer is 2530238.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We'll use symmetry and name classify same types of squares on basis on possible choices at the square, then, we'll use conditional probability.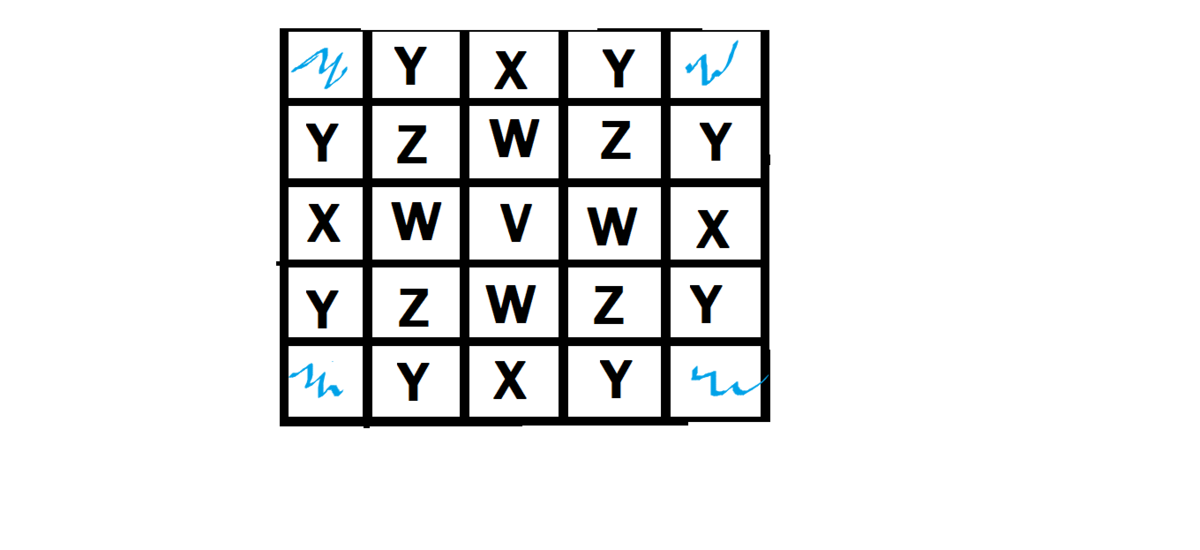 Choices:
Choices:
V -> 24
W -> 19
X -> 14
Y -> 11
Z -> 15
Let E ( i ) be the expected number of jumps taken from a type of square by toad to reach trap.
If we are on any of Z squares then we have 15 choices:
3Z,4W,4Y,2X,1V and 1 trap.
If we go to any of 3Z,4W,4Y,2X,1V our E ( Z ) will be set to respective E ( i ) +1, as we have made a jump to reach the square.
Similarly following this for all types of square we get following Equations:
E ( Z ) = ( 3 / 1 5 ) ( 1 + E ( Z ) ) + ( 4 / 1 5 ) ( 1 + E ( W ) ) + ( 4 / 1 5 ) ( 1 + E ( Y ) ) + ( 2 / 1 5 ) ( 1 + E ( X ) ) + ( 1 / 1 5 ) ( 1 + E ( V ) ) + ( 1 / 1 5 ) ( 1 )
E ( W ) = ( 1 / 1 9 ) ( 1 + E ( V ) ) + ( 3 / 1 9 ) ( 1 + E ( W ) ) + ( 4 / 1 9 ) ( 1 + E ( Z ) ) + ( 3 / 1 9 ) ( 1 + E ( X ) ) + ( 6 / 1 9 ) ( 1 + E ( Y ) ) + ( 2 / 1 9 ) ( 1 )
E ( V ) = ( 0 / 2 4 ) ( 1 + E ( V ) ) + ( 4 / 2 4 ) ( 1 + E ( W ) ) + ( 4 / 2 4 ) ( 1 + E ( Z ) ) + ( 4 / 2 4 ) ( 1 + E ( X ) ) + ( 8 / 2 4 ) ( 1 + E ( Y ) ) + ( 4 / 2 4 ) ( 1 )
E ( Y ) = ( 1 / 1 1 ) ( 1 + E ( V ) ) + ( 3 / 1 1 ) ( 1 + E ( W ) ) + ( 2 / 1 1 ) ( 1 + E ( Z ) ) + ( 2 / 1 1 ) ( 1 + E ( X ) ) + ( 2 / 1 1 ) ( 1 + E ( Y ) ) + ( 1 / 1 1 ) ( 1 )
E ( X ) = ( 1 / 1 4 ) ( 1 + E ( V ) ) + ( 3 / 1 4 ) ( 1 + E ( W ) ) + ( 2 / 1 4 ) ( 1 + E ( Z ) ) + ( 2 / 1 4 ) ( 1 + E ( X ) ) + ( 4 / 1 4 ) ( 1 + E ( Y ) ) + ( 2 / 1 4 ) ( 1 )
The needed expected value is:
E = ( 1 / 2 5 ) ( E ( V ) ) + ( 4 / 2 5 ) ( E ( W ) ) + ( 4 / 2 5 ) ( E ( Z ) ) + ( 4 / 2 5 ) ( E ( X ) ) + ( 8 / 2 5 ) ( E ( Y ) ) + ( 4 / 2 5 ) ( 0 )
Solving these equations we get: E = 2 7 9 0 7 5 2 2 5 1 1 6 3