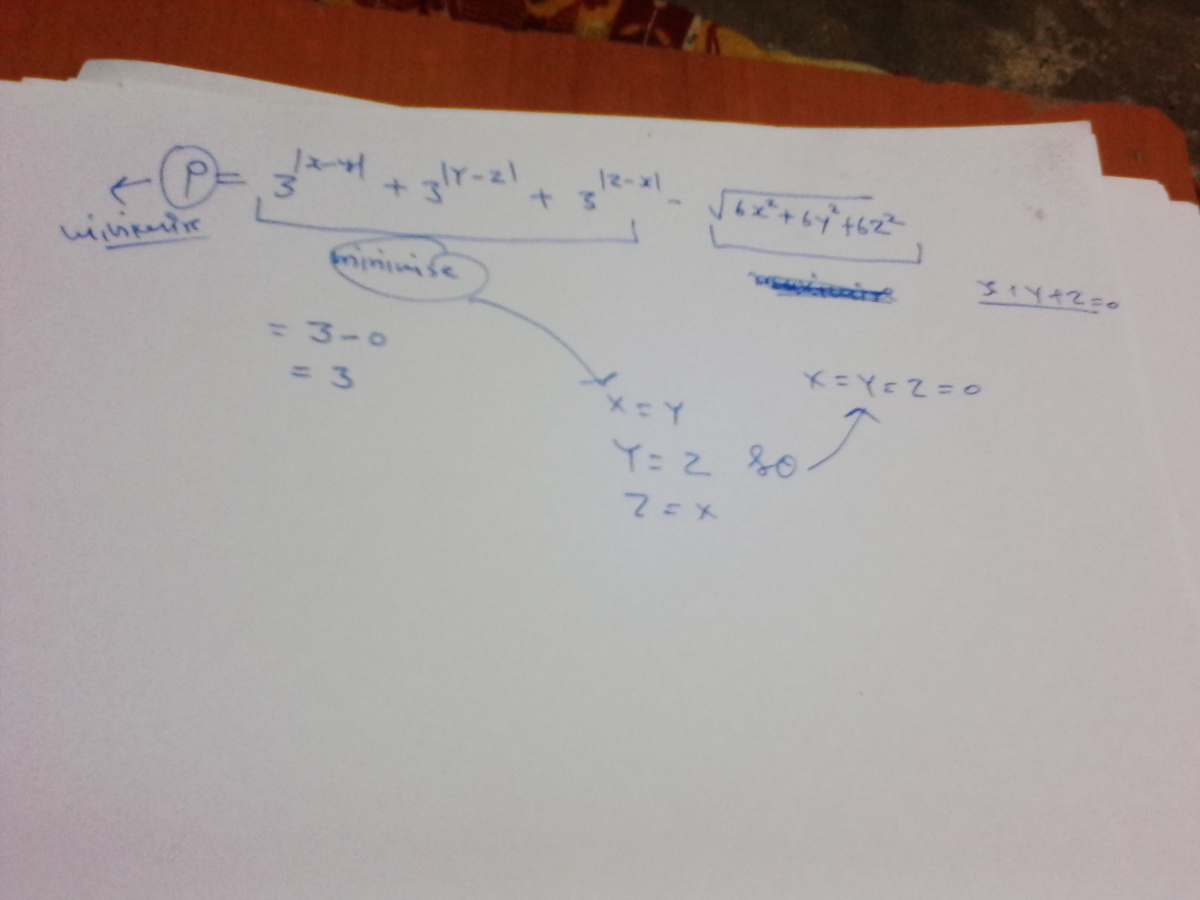Exponential maximum

Algebra Level 4

$\large { 3 }^{ | x-y | }+{ 3 }^{ | y-z | }+{ 3 }^{ | z-x | } - \sqrt{6x^2+6y^2+6z^2}$

Let $x, y$ and $z$ be real numbers satisfying $x + y + z = 0$ , find the minimum value of the expression above.

This problem is taken from the 2012 Vietnamese University Entrance Exam.

The answer is 3.0.

4 solutions

Jesus Ulises Avelar
Feb 27, 2015

What about maximizing x^2+y^2+z^2 for min p?

vijay katta - 6 years, 3 months ago

Yeah that also could work... The thing is that i thought would be easier this way so if you know how to do that, could you please post that solution.

Jesus Ulises Avelar - 6 years, 3 months ago

Yatharth Chowdhury
Feb 13, 2016

Its quite obvious that x , y and z = 0. If any one of them would have been non zero, then |x-y| , |y-z| and/or |z-x| ( and also x² , y² and z²) would be greater than 0 which would lead this sum to a much greater value than 3. Its common logic

Pulkit Gupta
Dec 1, 2015

The given equation is cyclic. Clearly then x= y = z. Here that implies that x = y = z = 0.

This leads us to our answer.

Devdutt Jiwan
May 30, 2015

Exponential maximum

This problem is taken from the 2012 Vietnamese University Entrance Exam.

The answer is 3.0.

4 solutions

0 pending reports