Exponential Wire Dynamics
Consider a particle of mass that can slide freely along the curve . At time the particle is at rest and is situated at the point . At the particle is released from rest. The goal of this problem is to compute the reaction force ( ) due to the wire acting on the particle as a function of . The expression is of the form:
Here , , and are positive integers. Compute .
Note:
-
An ambient constant gravitational field along the negative Y direction exists throughout space. Acceleration due to gravity is .
-
is the Euler's number.
-
This problem has been reposted and older versions have been deleted.
Bonus:
- Evaluate:
Does the result make sense?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
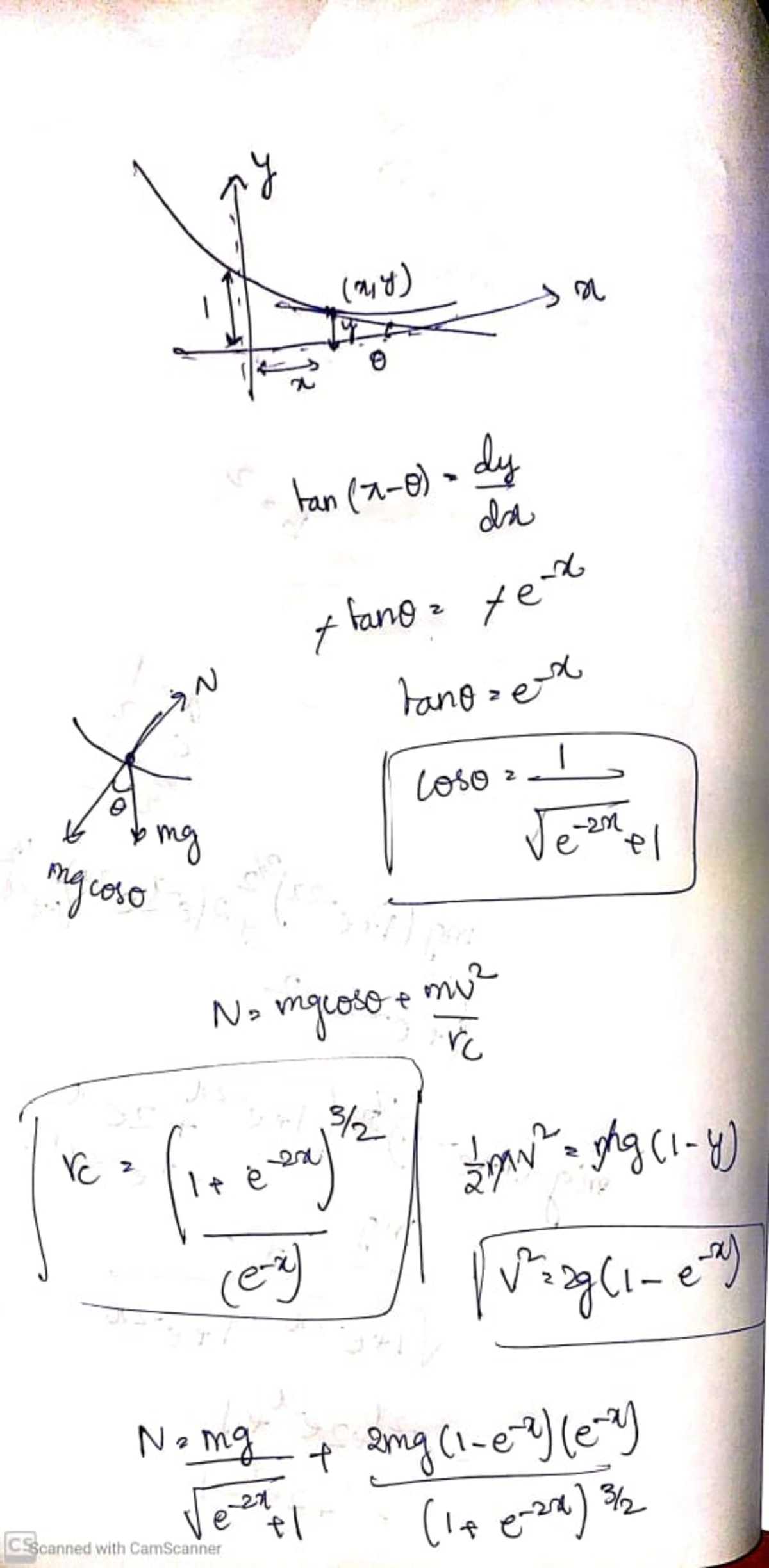
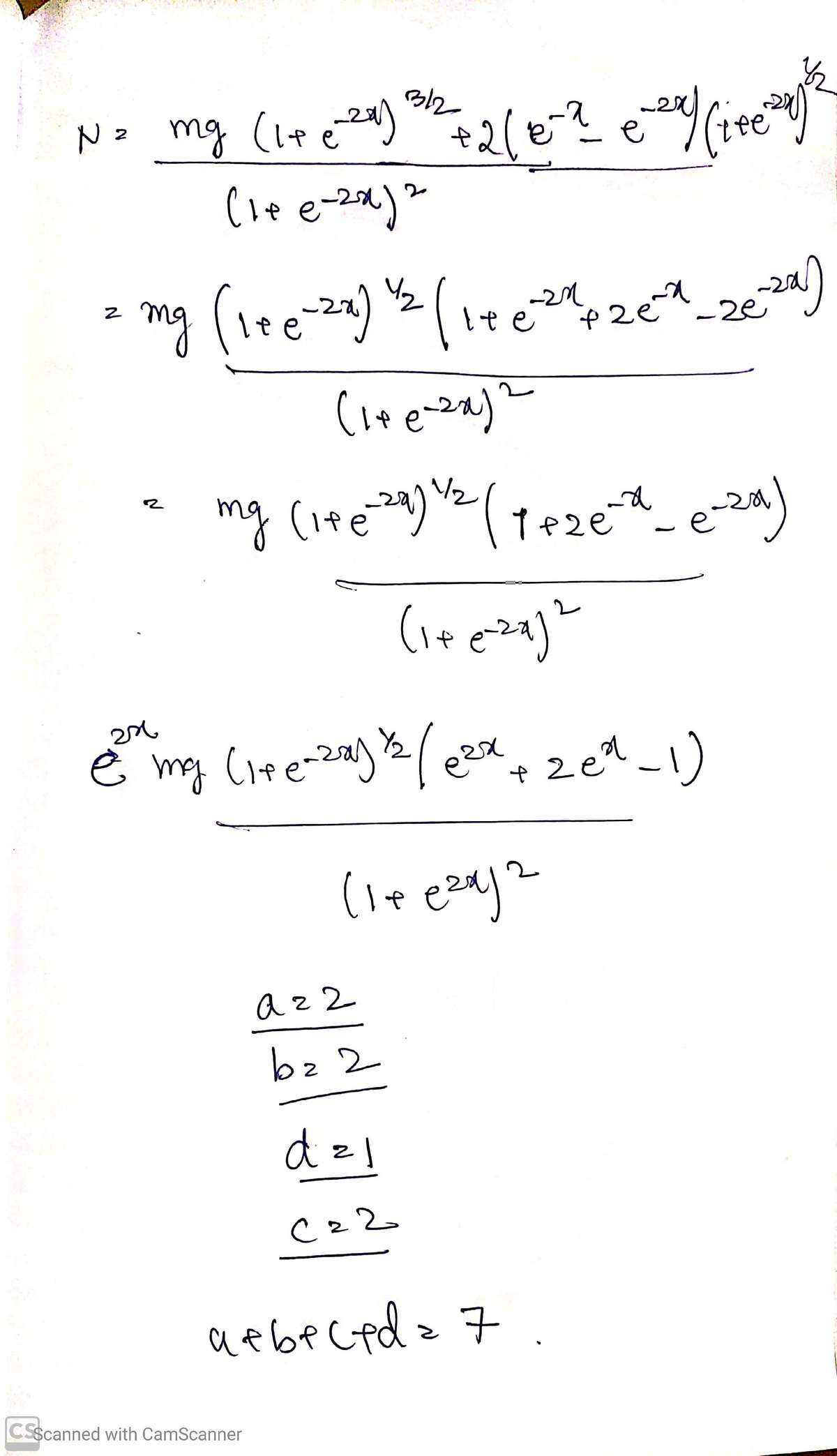
y = e − x ⟹ d x d y = − e − x , d x 2 d 2 y = e − x .
So, cos α = 1 + e − 2 x 1 , ρ = d x 2 d 2 y ( 1 + ( d x d y ) 2 ) 2 3 = e − x ( 1 + e − 2 x ) 2 3 ,
where α is the angle subtended by the tangent to the curve y = e − x at ( x , e − x ) with the negative x -axis and ρ is the radius of curvature of this curve at that point.
Normal reaction offered by the curve on the particle is
N ( x ) = m g cos α + ρ m v 2 .
The velocity v of the particle at that point is determined by using the energy conservation principle :
m g ( 1 − y ) = 2 1 m v 2 ⟹ m v 2 = 2 m g ( 1 − e − x ) ⟹
N ( x ) = ( 1 + e − 2 x ) 2 3 m g ( 1 + 2 e − x − e − 2 x ) =
( 1 + e 2 x ) 2 m g e 2 x 1 + e − 2 x ( e 2 x + 2 e x − 1 ) .
So, a = 2 , b = 2 , c = 2 , d = 1 and a + b + c + d = 7 .
In the limit when x approaches infinity, N ( x ) tends to m g , which is quite natural, since in that limit the curve flattens to a straight line parallel to the x -axis, assymptotically meeting the axis, so that curvature of the curve and hence the centrifugal force becomes zero, and the component of weight force generating the normal reaction is m g .