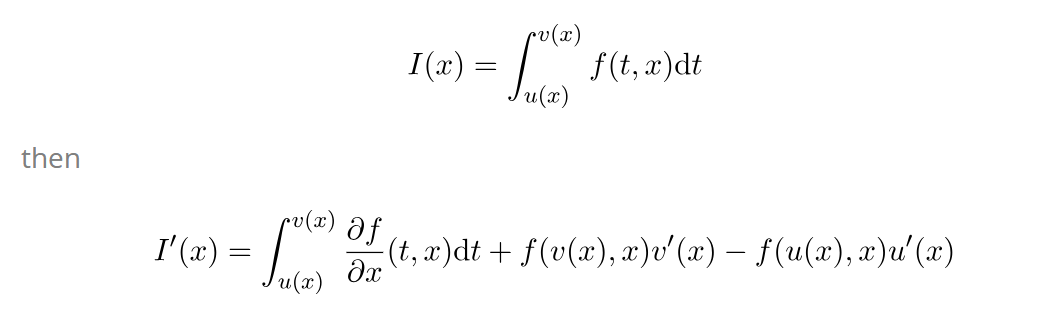Exponentially sinusoidal
Consider the function
Let , , and respectively be the coefficients of , , and in the first order differential equation of .
where it is also given that is positive .
further can be expressed as follows
Then evaluate
Note that are real numbers and they have no common factor
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
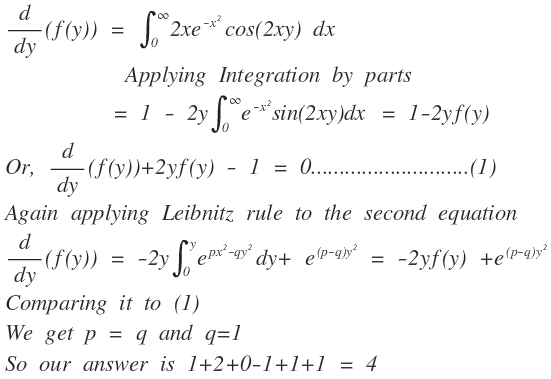 for Leibnitz Rule see below :-
for Leibnitz Rule see below :-