Extend it
 Triangle
A
B
C
is inscribed in a circle with center at
O
of radius
3
. Given that
∠
C
A
B
=
4
5
∘
and
A
B
=
3
, find
A
C
correct to three decimal places.
Triangle
A
B
C
is inscribed in a circle with center at
O
of radius
3
. Given that
∠
C
A
B
=
4
5
∘
and
A
B
=
3
, find
A
C
correct to three decimal places.
The answer is 5.796.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
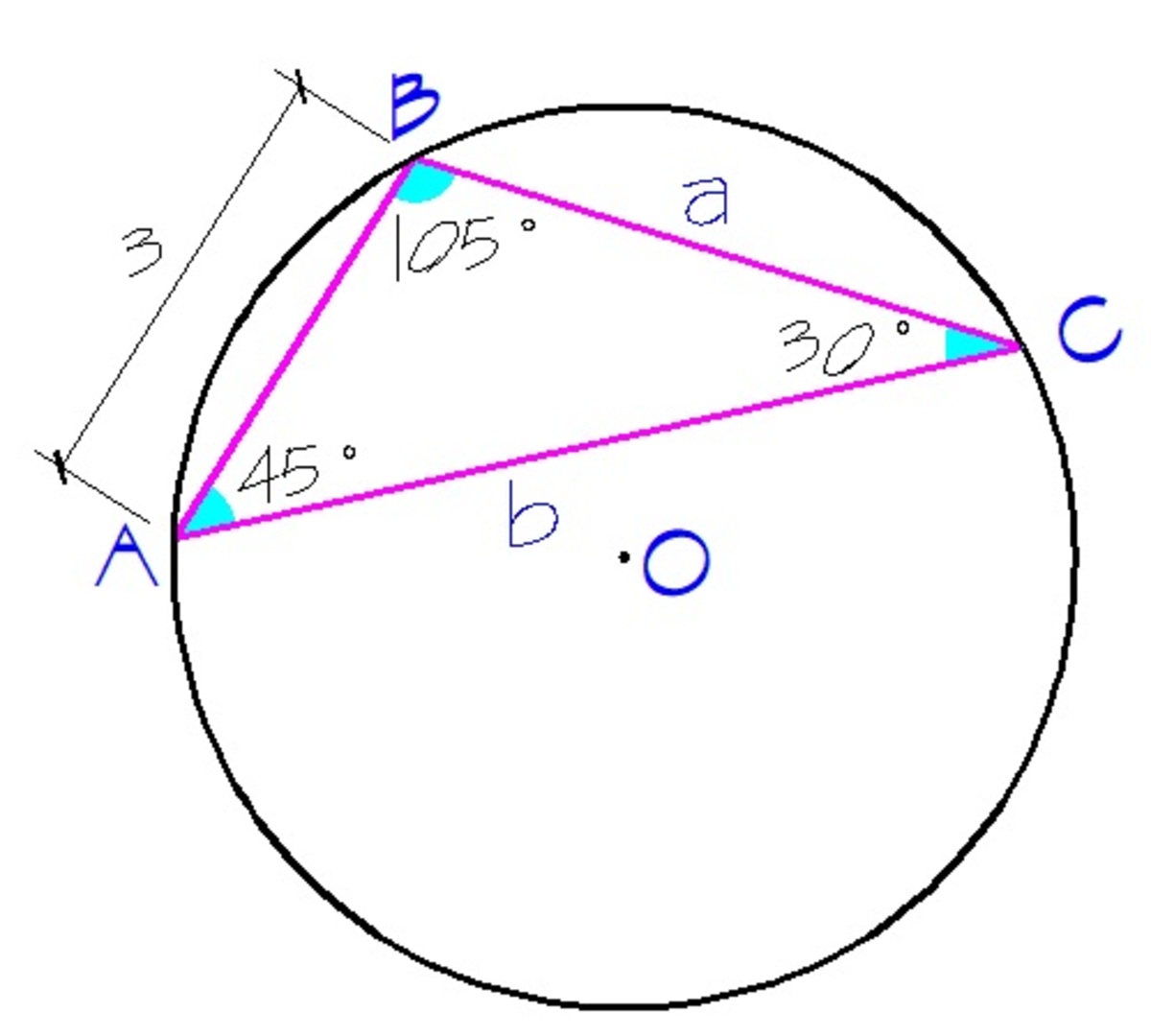 By the extended law of sines, we have
By the extended law of sines, we have
sin C 3 = 2 R ⟹ sin C 3 = 2 ( 3 ) ⟹ C = sin − 1 ( 6 3 ) = 3 0 ∘
It follows that B = 1 8 0 − 4 5 − 3 0 = 1 0 5 ∘ .
By extented law of sines again, we have
sin 1 0 5 b = 2 R ⟹ sin 1 0 5 b = 2 ( 3 ) ⟹ b = ( sin 1 0 5 ) ( 6 ) ≈ 5 . 7 9 6
What's the extended law of sine if in might ask? I used the law of sine 2, but only once in triangle AOC.
Since AB=3, it follows that triangle AOB has the same side lengths so every angle is 60 degree. This gives angle OAC = OCA = 15 degrees, leading to AOC = 150 degrees. Using law of sine in triangle AOC gives AC.