Extend the Pattern
How many cubes will be in the 43rd item in this series?
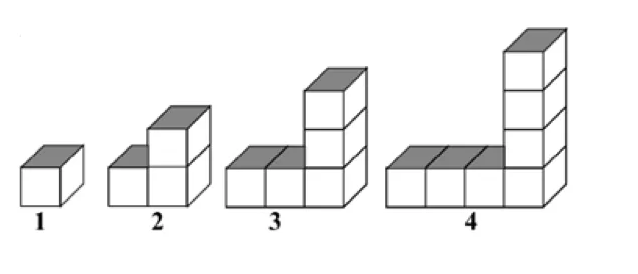
The answer is 85.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
We just notice that the total of cubes in each figure represents the sum of the cubes of that figure and the preceding one, for instance, in figure 4, it is 4+3=7 cubes. Hence, in figure 43, the total number of cubes is 43+42= 85
so how we arrive at 1? is 0 is part of this pattern? looking to your answer.
Log in to reply
0 cube means that there was no cube. We started with 1 cube and went on. The question is asking how many cubes are there in the 43rd figure. It means we started with one cube and built more cubes on top of it until we reached figure numbered 43. We need to decide by then how many cubes are there in this figure? From the given figures, we can deduce a pattern and make a generalization.
As we can see, the sequence 1,3,5,7,... appears to be a arithmetic sequence. So we can use in finding an n t h t e r m by using the following equation: a n = a 1 + ( n − 1 ) d .
Whereas, a n is the 1st term which is 1.
And, n as the no. of terms which is 43.
And, d as the common difference of each preceding or succeeding term, which is 2 as 3-1=2.
Pluging in the values,
a n = 1 + ( 4 3 − 1 ) 2
a n = 1 + 8 4
a n = 8 5
Therefore, the 43rd term is 8 5 .
Suppose the cube pattern is 1-43 ,i.e 1,2,3,4,5...41,42,43 than the answer will be 43 . 1,2,3,4,5...41,42,43 ------( eq. I) converting the (equation I) into given pattern 1,3,5,7... 1 , 2 , 3 , 4 , 5 .......41, 42 , 43 (0 ,+1, +2,+3,+4....+40,+41,+42) =1,3,5,7,9...............81,83,85 (question pattern ) The answer will be 85.
The first term has a height of one cube, second term has two cubes, third has four cubes and so on. The length is equal to height minus one cube because it is used by the height. So, the 43rd term has 43+(43-1) or 85 cubes.
Relevant wiki: Identifying Pattern Relationships
The pattern of the total number of blocks is 1 , 3 , 5 , 7 . . . Inspecting the first four terms, we see that for the n t h item, the total number of blocks ( t ) can be determined as follows: t = n ∗ 2 − 1
1st term, n=1: 1 ∗ 2 − 1 = 1
2nd term, n=2: 2 ∗ 2 − 1 = 3
n=3: 3 ∗ 2 − 1 = 5
n=4: 4 ∗ 2 − 1 = 7
n=43: 4 3 ∗ 2 − 1 = 8 5