Extended Bisector
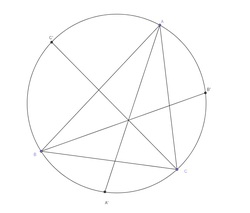 Triangle
A
B
C
is inscribed in a unit circle. The three bisectors of the angle
A
,
B
and
C
are extended to intersect the circle at
A
′
,
B
′
and
C
′
respectively. Determine the value of
Triangle
A
B
C
is inscribed in a unit circle. The three bisectors of the angle
A
,
B
and
C
are extended to intersect the circle at
A
′
,
B
′
and
C
′
respectively. Determine the value of
sin A + sin B + sin C A A ′ cos 2 A + B B ′ cos 2 B + C C ′ cos 2 C
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Observe that A ′ B = A ′ C = 2 cos 2 A a . By Ptolemy's Theorem, A B ⋅ A ′ C + A C ⋅ A ′ B = A A ′ ⋅ B C . Substitution and rearrangement yield A A ′ cos 2 A = 2 b + c and similarly for B B ′ and C C ′ . Therefore, the desired sum is sin A + sin B + sin C 2 b + c + 2 c + a + 2 a + b = sin A + sin B + sin C a + b + c . By the Extended Law of Sines, a = 2 sin A and similarly for b and c , so the answer is 2 .
With equilateral triangle, denote R is radius of circumscribed circle. it has: A A ′ = B B ′ = C C ′ = 2 R , s i n A = s i n B = s i n C = c o s ( 2 A ) = c o s ( 2 B ) = c o s ( 2 C ) = 2 3 ⇒ R e s u l t = 2 3 3 3 3 = 2
Well, a short way to do it can be to assume the triangle to be equilateral... The expression then reduces to 2 R Where R is the radius of the circumcircle , which here is "1" Hence answer = 2
By observing triangle A B A ′ , we have sin ( B + 2 1 A ) A A ′ = 2 r = 2 × 1 = 2 ⟹ A A ′ = 2 sin ( B + 2 1 A )
The same process for triangle B C B ′ and C A C ′ , we have B B ′ = 2 sin ( C + 2 1 B ) and C C ′ = 2 sin ( A + 2 1 C )
Then, sin A + sin B + sin C A A ′ cos 2 A + B B ′ cos 2 B + C C ′ cos 2 C is
= sin A + sin B + sin C 2 sin ( B + 2 1 A ) cos 2 A + 2 sin ( C + 2 1 B ) cos 2 B + 2 sin ( A + 2 1 C ) cos 2 C = sin A + sin B + sin C sin ( B + A ) + sin B + sin ( C + B ) + sin C + sin ( A + C ) + s i n A = sin A + sin B + sin C sin ( 1 8 0 − C ) + sin ( 1 8 0 − A ) + sin ( 1 8 0 − B ) + sin A + sin B + sin C = sin A + sin B + sin C 2 ( sin A + sin B + sin C ) = 2 2 sin A cos B = sin ( A + B ) + sin ( A − B ) A + B + C = 1 8 0