Extended Triangle-ception
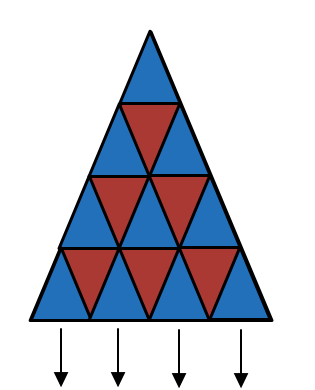 The diagram shows the tiling of the first
smallest congruent equilateral triangles.
The diagram shows the tiling of the first
smallest congruent equilateral triangles.
The extension of this triangle has a total of smallest congruent equilateral triangles.
Find the positive value of if the total number of triangles (of all sizes) for this diagram is 988.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The general formula for the total number of triangles as a function of n is
f ( n ) = ⌊ 8 n ( n + 2 ) ( 2 n + 1 ) ⌋ , as found here .
The proof of this formula is quite involved. A discussion on this general problem, with a variety of approaches, can be found here .
To solve for n in this problem, I first made an initial estimate using the approximation
2 n 3 = 8 ∗ 9 8 8 ⟹ n = 1 5 . 8 1 to 2 decimal places.
I knew this estimate would be on the high side, so I tried f ( 1 5 ) to find that
f ( 1 5 ) = ⌊ 8 7 9 0 5 ⌋ = ⌊ 9 8 8 . 1 2 5 ⌋ = 9 8 8 , and thus concluded that n = 1 5 .