Extension and new area - Most General Case

We can cut the triangle as in the previous problems, or we can use barycentric coordinates.

Let $A=(1,0,0),B=(0,1,0),C=(0,0,1)$ , then $B'=(-b,1+b,0), C'=(0,-c,1+c), A'=(1+a,0,-a)$ .

The ratio of the areas can be expressed as a determinant $\text{det} \left(\begin{array}{c}1+a & 0 & -a\\-b & 1+b & 0\\ 0&-c&1+c\end{array}\right)$

This simplfies to $(a+1)(b+1)(c+1)-abc=1+a+b+c+ab+bc+ca$

Let $AB=x$ , $BC=y$ , $CA=z$ . Then, $BB'=bx$ , $CC'=cy$ , $AA'=az$ .

Moreover, let $\left[ {ABC} \right] = S$ , $\left[ {BB'C'} \right] = {S_1}$ , $\left[ {CC'A'} \right] = {S_2}$ , $\left[ {AA'B'} \right] = {S_3}$ and $\left[ {A'B'C'}\right]=S'$ .

Then,
$\frac{{{S_1}}}{S} = \frac{{\bcancel{{\frac{1}{2}}}BB' \cdot BC' \cdot \cancel{{\sin \left( {180^\circ - \theta } \right)}}}}{{\bcancel{{\frac{1}{2}}}BA \cdot BC \cdot \cancel{{\sin \theta }}}} = \frac{{bx \cdot \left( {y + cy} \right)}}{{x \cdot y}} = \frac{{bxy\left( {1 + c} \right)}}{{xy}} = b + bc$ Similarly, $\frac{{{S_2}}}{S} = \frac{{\frac{1}{2}CC' \cdot CA' \cdot \sin \left( {180^\circ - \varphi } \right)}}{{\frac{1}{2}CB \cdot CA \cdot \sin \varphi }} = \frac{{cy \cdot \left( {z + az} \right)}}{{y \cdot z}} = \frac{{cyz\left( {1 + a} \right)}}{{yz}} = c + ca$ $\frac{{{S_3}}}{S} = \frac{{\bcancel{{\frac{1}{2}}}AA' \cdot AB' \cdot \cancel{{\sin \left( {180^\circ - \omega } \right)}}}}{{\bcancel{{\frac{1}{2}}}AC \cdot AB \cdot \cancel{{\sin \omega }}}} = \frac{{az \cdot \left( {x + bx} \right)}}{{z \cdot x}} = \frac{{azx\left( {1 + b} \right)}}{{zx}} = a + ab$

Adding,

$\frac{{{S_1} + {S_2} + {S_3}}}{S} = a + b + c + ab + bc + ca$

Hence,

$\frac{{S'}}{S} = \frac{{S' - S}}{S} + 1 = \frac{{{S_1} + {S_2} + {S_3}}}{S} + 1 = \boxed{1 + a + b + c + ab + bc + ca}.$

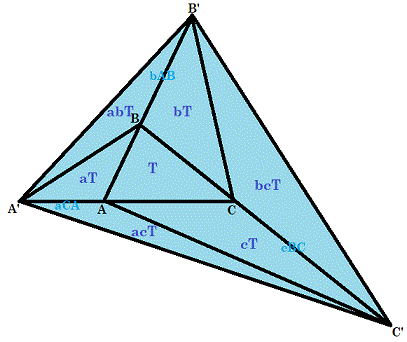
Let $T$ be the area of $\triangle ABC$ .

If $AA' = aCA$ , then $\triangle BAA'$ has the same height as $\triangle ABC$ but a base of $aCA$ instead of $CA$ , so $\triangle BAA'$ has an area of $aT$ .

If $BB' = bAB$ , then $\triangle CBB'$ has the same height as $\triangle ABC$ but a base of $bAB$ instead of $AB$ , so $\triangle CBB'$ has an area of $bT$ .

If $CC' = cBC$ , then $\triangle ACC'$ has the same height as $\triangle ABC$ but a base of $cBC$ instead of $AB$ , so $\triangle ACC'$ has an area of $cT$ .

Also if $AA' = aCA$ , then $\triangle C'AA'$ has the same height as $\triangle ACC'$ but a base of $aCA$ instead of $CA$ , so $\triangle C'AA'$ has an area of $acT$ .

Also if $BB' = bAB$ , then $\triangle A'BB'$ has the same height as $\triangle BAA'$ but a base of $bAB$ instead of $AB$ , so $\triangle A'BB'$ has an area of $abT$ .

Also if $CC' = cBC$ , then $\triangle B'CC'$ has the same height as $\triangle CBB'$ but a base of $cBC$ instead of $BC$ , so $\triangle B'CC'$ has an area of $bcT$ .

Therefore, the ratio of areas of $\triangle A'B'C'$ to $\triangle ABC$ is $\frac{T + aT + bT + cT + abT + acT + bcT}{T} = \boxed{1 + a + b + c + ab + ac + bc}$ .