Extension in Spring due to Magnetic force!
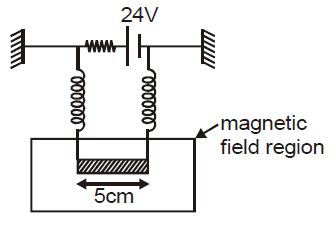 The circuit in figure consists of wires at the top and bottom and identical metal springs as the left and right sides. The wire at the bottom has a mass of
and is
long. The wire is hanging as shown in the figure. The spring stretch
under the weight of the wire and the circuit has a total resistance of
. When the lower wire is subjected to a static magnetic field, the springs stretch an additional
. The magnetic field is?
The circuit in figure consists of wires at the top and bottom and identical metal springs as the left and right sides. The wire at the bottom has a mass of
and is
long. The wire is hanging as shown in the figure. The spring stretch
under the weight of the wire and the circuit has a total resistance of
. When the lower wire is subjected to a static magnetic field, the springs stretch an additional
. The magnetic field is?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Draw The FBD of the system.
When magnetic field is on, in equilibrium, K Δ L = m g + B i L
⇒ B = i L K Δ L − m g = R V L ( Δ l 0 m g Δ l − m g ) (where Δ l 0 is the expansion when no magnetic field is on.)
Magnetic field must be of out of the page as magnetic force is downward.