Extension!
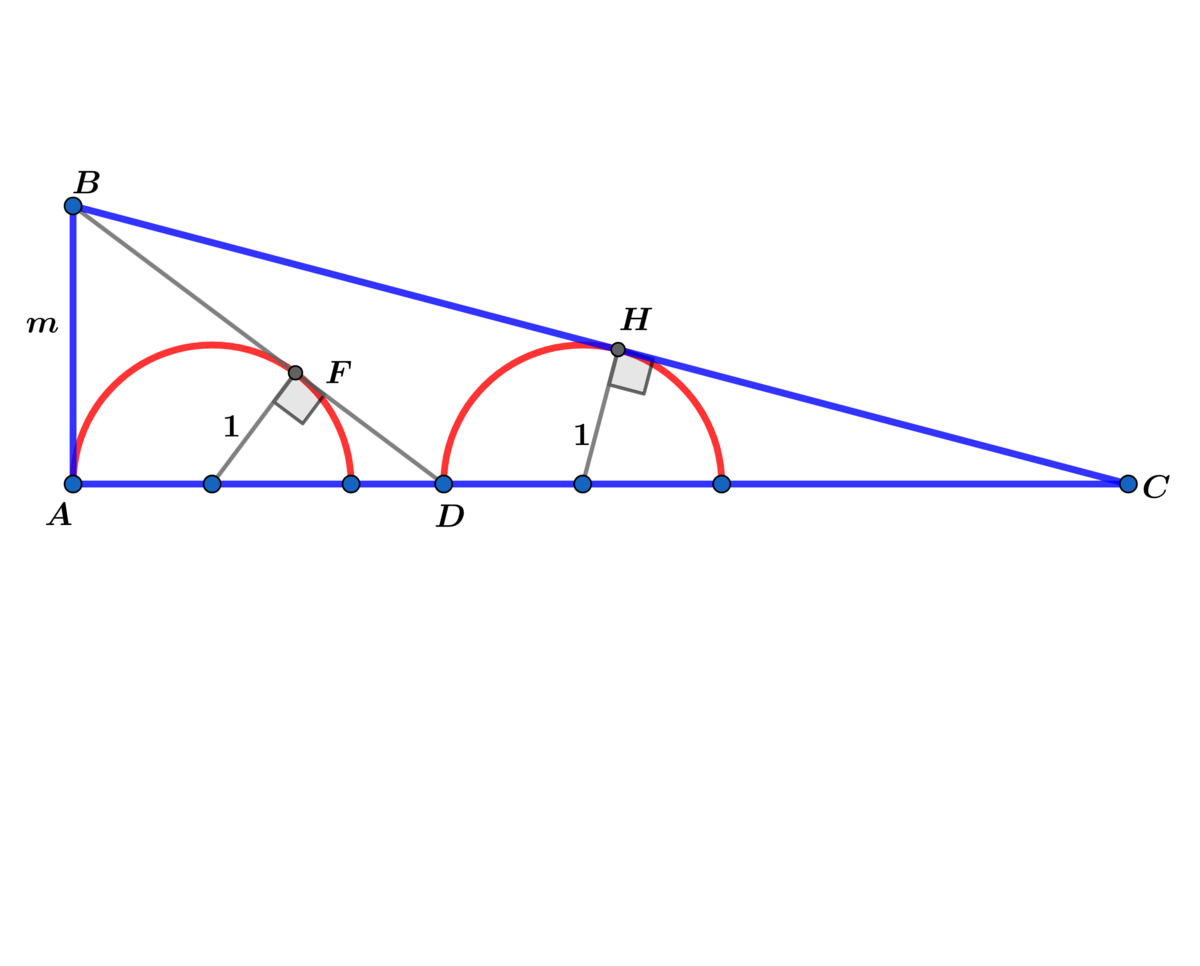
Let .
In right with , and are tangent to the two inscribed unit semicircles at and respectively.
Extend the above diagram to congruent unit circles as follows:
Draw another unit semicircle through C and construct the tangent from B and mark the intersection with the extended line AC and continue this process for the unit semicircles.
(1) Find a formula for the area of the right triangle formed which contains the unit semicircles.
(2) Using and write a program to compute the area of .
Below is a diagram for the area of
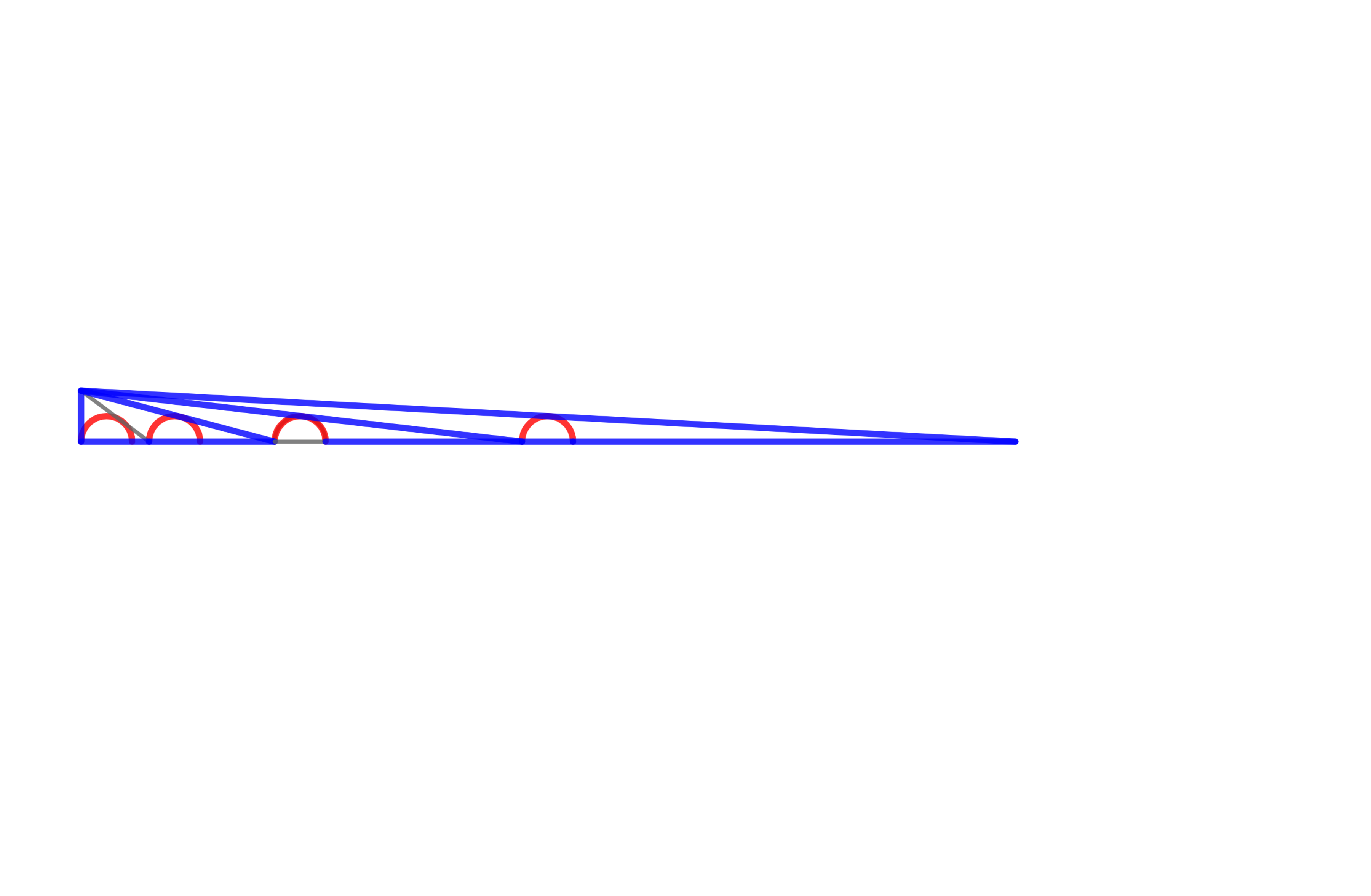
The answer is 2473.00493680999.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let m > 1 .
△ A B D ∼ △ E F D ⟹ m = y 1 B D ⟹ B D = m y 1
Using the Pythagorean theorem on △ A B D ⟹ m 2 y 1 2 = m 2 + ( 1 + y 1 ) 2 ⟹
( m 2 − 1 ) y 1 2 − 2 y 1 − ( m 2 + 1 ) = 0 ⟹ y 1 = m 2 − 1 m 2 + 1 ⟹
d 1 = A D = m 2 − 1 2 m 2 ⟹ A 1 = m 2 − 1 m 3 .
d 1 = m 2 − 1 2 m 2 ⟹ m 2 + ( d 1 + 1 + y 2 2 ) 2 = m 2 y 2 2 ⟹
( m 2 − 1 ) y 2 2 − 2 ( d 1 + 1 ) y 2 − ( m 2 + ( d 1 + 1 ) 2 ) = 0 ⟹
y 2 = m 2 − 1 d 1 + 1 + m ( d 1 + 1 ) 2 + m 2 − 1
d 2 = d 1 + 1 + y 2 = m 2 − 1 m ( ( d 1 + 1 ) m + ( d 1 + 1 ) 2 + m 2 − 1 )
Similarly m 2 + ( d 2 + 1 + y 3 ) 2 = m 2 y 3 2 ⟹
( m 2 − 1 ) y 3 2 − 2 ( d 2 + 1 ) y 3 − ( m 2 + ( d 2 + 1 ) 2 ) = 0 ⟹
y 3 = m 2 − 1 d 2 + 1 + m ( d 2 + 1 ) 2 + m 2 − 1 ⟹
d 3 = d 2 + 1 + y 3 = d 2 + 1 + y 3 = m 2 − 1 m ( ( d 2 + 1 ) m + ( d 2 + 1 ) 2 + m 2 − 1 )
In General using A 1 = m 2 − 1 m 3
Let d 1 = m 2 − 1 2 m 2
and for n ≥ 1 define:
d n + 1 = m 2 − 1 m ( ( d n + 1 ) m + ( d n + 1 ) 2 + m 2 − 1 ) and A n + 1 = 2 m d n + 1
or if you prefer d n + 1 = m 2 − 1 m ( ( d n + 1 ) m + d n 2 + 2 d n + m 2 ) and A n + 1 = 2 m d n + 1
Using the above recursive formula with m = 2 the program below computes A 1 0 using python:
0
⟹ A 1 0 = 2 4 7 3 . 0 0 4 9 3 6 8 0 9 9 9 .