Extensions of a triangle
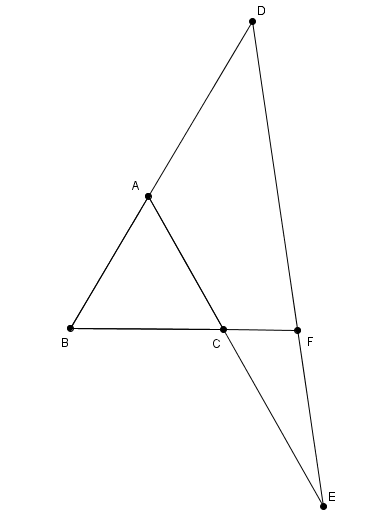 Let be
A
B
C
an equilateral triangle of side
1
.
D
and
E
points on the extension of
A
B
and
A
C
, respectively such that
A
D
=
C
E
=
1
.
F
is the point of interseccion between
D
E
and
B
C
extension.
Let be
A
B
C
an equilateral triangle of side
1
.
D
and
E
points on the extension of
A
B
and
A
C
, respectively such that
A
D
=
C
E
=
1
.
F
is the point of interseccion between
D
E
and
B
C
extension.
Find the length C F to 3 decimal places.
The answer is 0.333333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
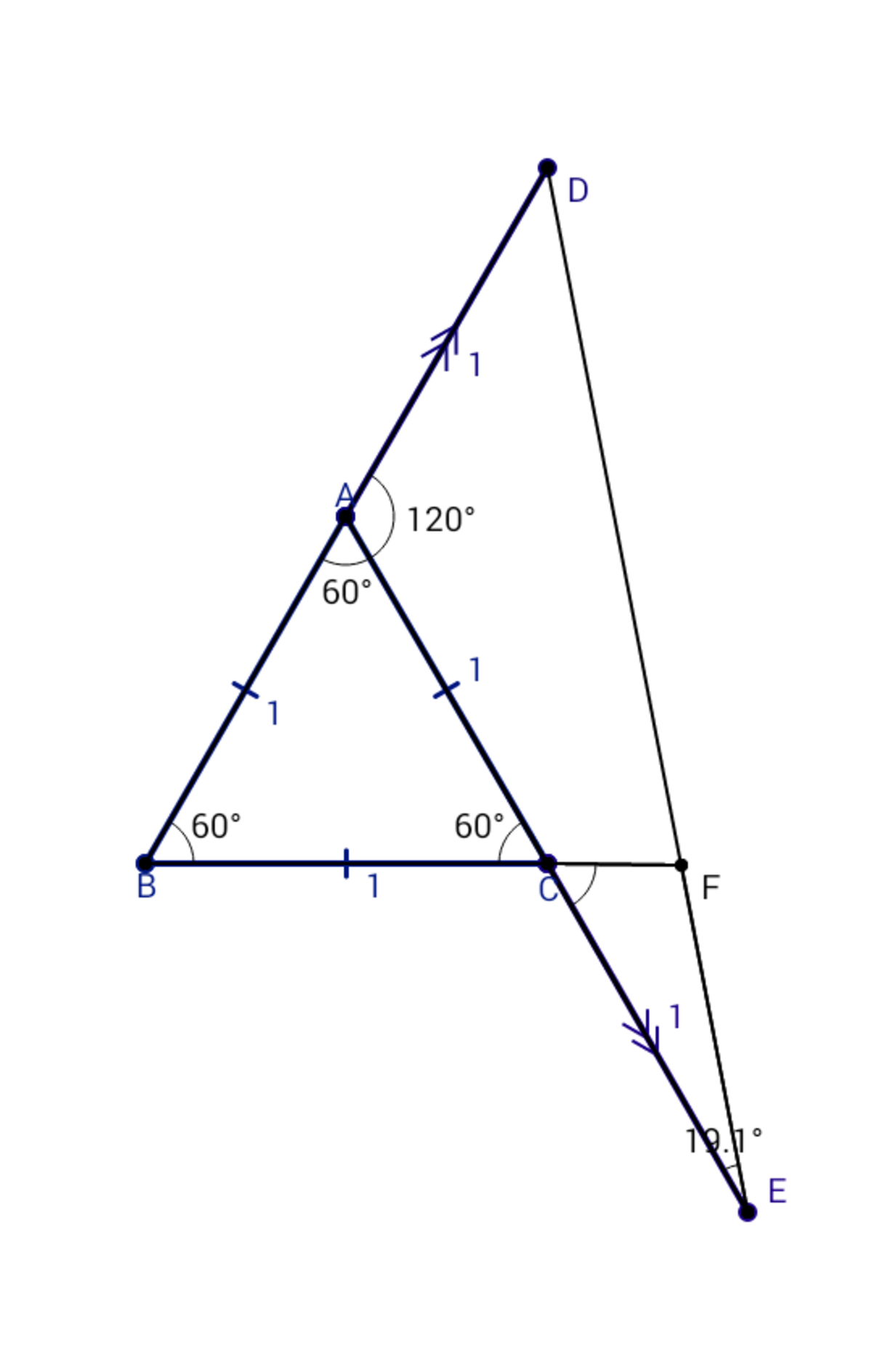
Let, ∠ C E F = θ & ∠ C F E = α
From the law of cosine we get, D E = 1 2 + 2 2 + 2 × 1 × 2 cos 1 2 0 ∘ = 7 From the law of sine we get, sin 1 2 0 ∘ 7 = sin θ 1 ⇒ θ = 1 9 . 1 1 ∘ So, α = 1 8 0 ∘ − ( 6 0 ∘ + 1 9 . 1 1 ∘ ) = 1 0 0 . 8 9 ∘ Applying the law of sine one last time we get, sin 1 9 . 1 1 ∘ C F = sin 1 0 0 . 8 9 ∘ 1 ⇒ C F = sin 1 0 0 . 8 9 ∘ sin 1 9 . 1 1 ∘ ≈ 0 . 3 3 3
Hi-Five, I used exactly this same method!!
Draw a parallel by BF from A to DE at M. Then you see 2AM=BF & 2BF=AM. so you will see BF = 0.333.
Applying the theorem of Menelaus of Alexandria ( Menelaus' Theorem ), we have
E C A E ⋅ F B C F ⋅ A D B D = 1
1 2 ⋅ 1 + C F C F ⋅ 1 2 = 1
1 + C F 4 C F = 1
3 C F = 1
C F = 3 1 ≈ 0 . 3 3 3 3 3 3 3
J o i n D C . I n Δ D B C , D B = 2 , B C = 1 , ∠ D B C = 6 0 . ∴ ∠ B C D = 9 0 , a n d D C = 3 . Δ D C E , D C = 3 , C E = 1 , ∠ D C E = 9 0 + 6 0 = 1 5 0 . L e t ∠ E D C = α . s o ∠ C E D = 3 0 − α . B y S i n R u l e 3 S i n ( 3 0 − α ) = 1 S i n ( α ) . E x p a n d i n g S i n o f s u m a n d s i m p l i f y i n g , C o t ( α ) = 3 3 = C F D C . ⟹ C F = 3 3 3 = . 3 3 3 3 3 3
△ D A C is isosceles with A D = A C = 1 and ∠ D A C = 1 2 0 ° ∠ A C D = ∠ A D C = 3 0 ° ⇒ ∠ D C B = 9 0 ° and △ D C B is 3 0 ° − 9 0 ° − 6 0 ° ∴ D C = 3 .
Then extend D C and draw a parallel by E to B C which cuts D C , as image shows. △ C E G is 3 0 ° − 6 0 ° − 9 0 ° with C E = 1 ∴ C G = 2 3 and G E = 2 1 .
△ D C F ∼ △ D G E ⇒ D G D C = G E C F → 2 3 3 3 = 2 1 C F ⇒ C F = 3 2 × 2 1 = 3 1 ≈ 0 . 3 3 3