Extraordinary Polynomial
a x 3 + b x 2 + c x + d is a cubic polynomial,
where ( a , b , c , d ) ϵ N
has real roots x 1 , x 2 , x 3
such that ,
f ( 2 ) = 1 4 0
f ( 3 ) = 2 4 0
f ( 5 ) = 5 6 0
f ( 7 ) = 1 0 8 0
Then evaluate ,
( ∑ i = 1 3 2 + x i ) + ( ∑ i = 1 3 3 + x i ) + ( ∑ i = 1 3 5 + x i )
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
solve simultinious eqns by subtracting the nth line from the n+1 line and multiplying/ dividing to make elimination easiear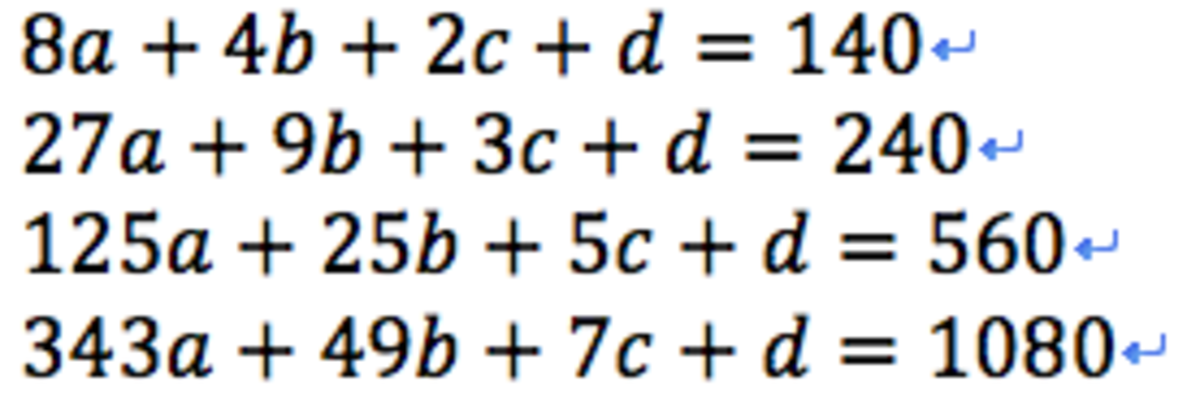
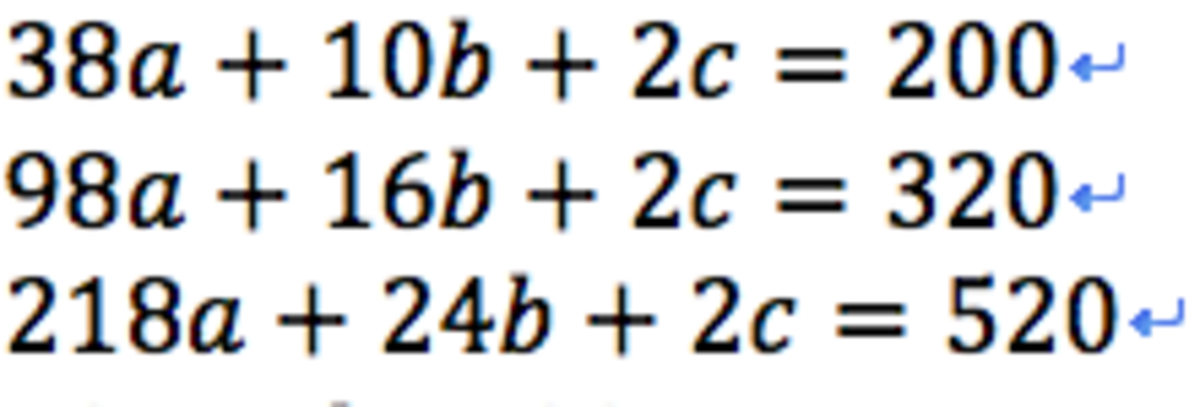
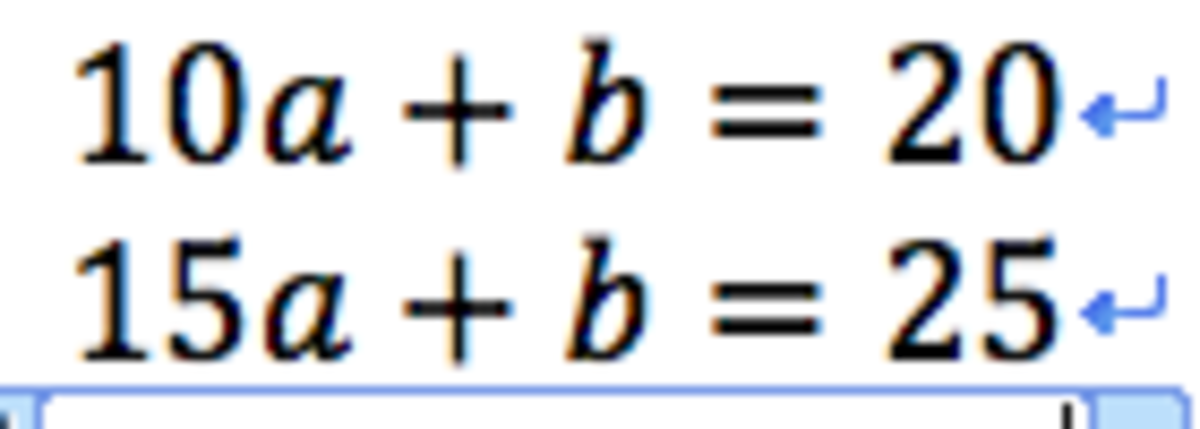
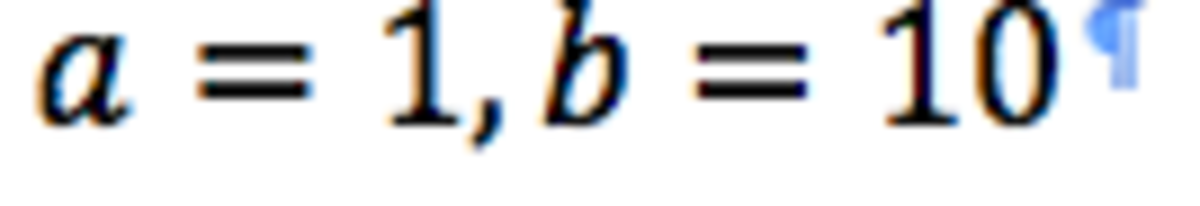 by vietas we are looking for
by vietas we are looking for
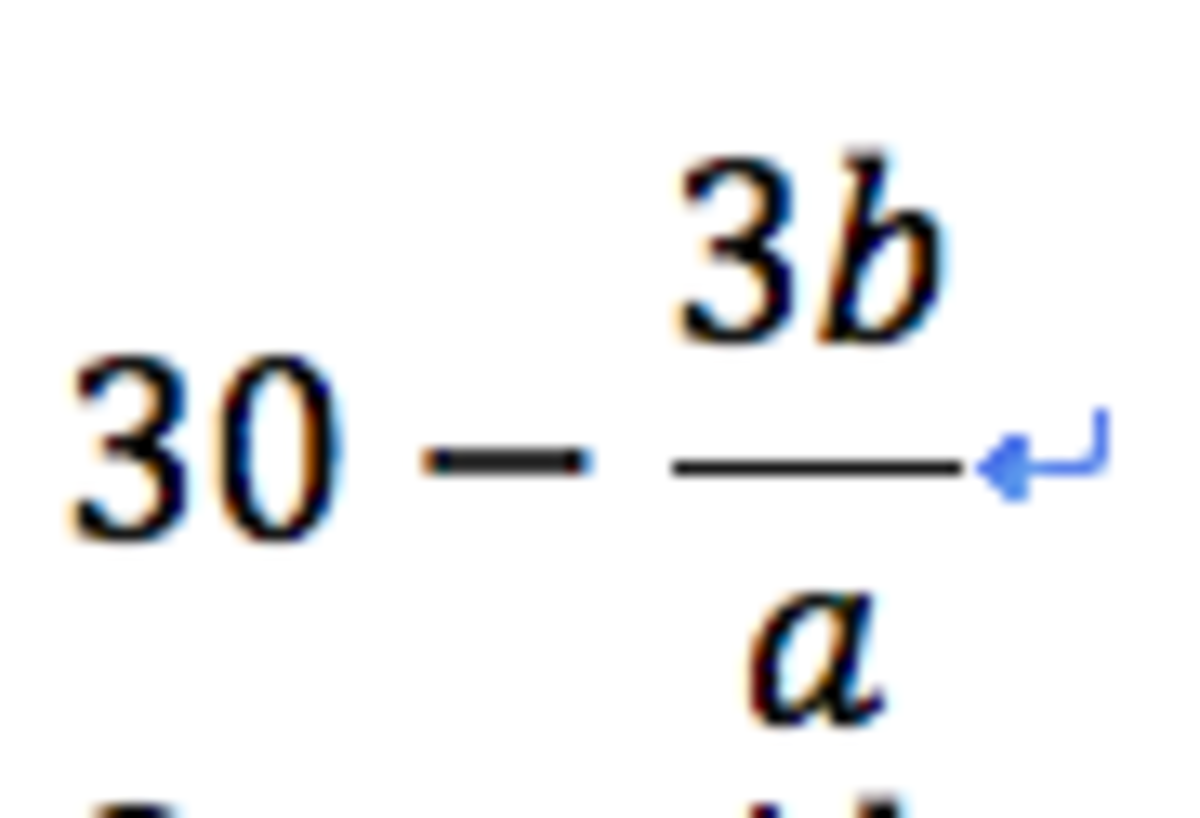 which is 30-30=
0
which is 30-30=
0