Extreme Value with Triangle 2.2
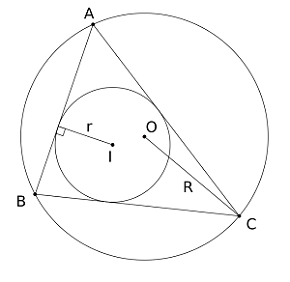
In the diagram, let and be the circumradius and inradius (the radii of the circumscribed circle and inscribed circle) of respectively, and
Find the maximum value of
The answer is 0.875.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since cos θ decreases with θ , cos A is maximum when ∠ A is minimum. This occurs when vertex A is farthest away from I when ∠ A subtends the smallest arc B C . That is vertex A is at the end farther away from I of the diameter of circumcircle joining O , I and A (see figure).
We note that sin 2 A = 1 2 3 = 4 1 . Therefore cos A = 1 − 2 sin 2 2 A = 1 − 2 ( 4 1 ) 2 = 8 7 = 0 . 8 7 5