Extreme Value with Triangle
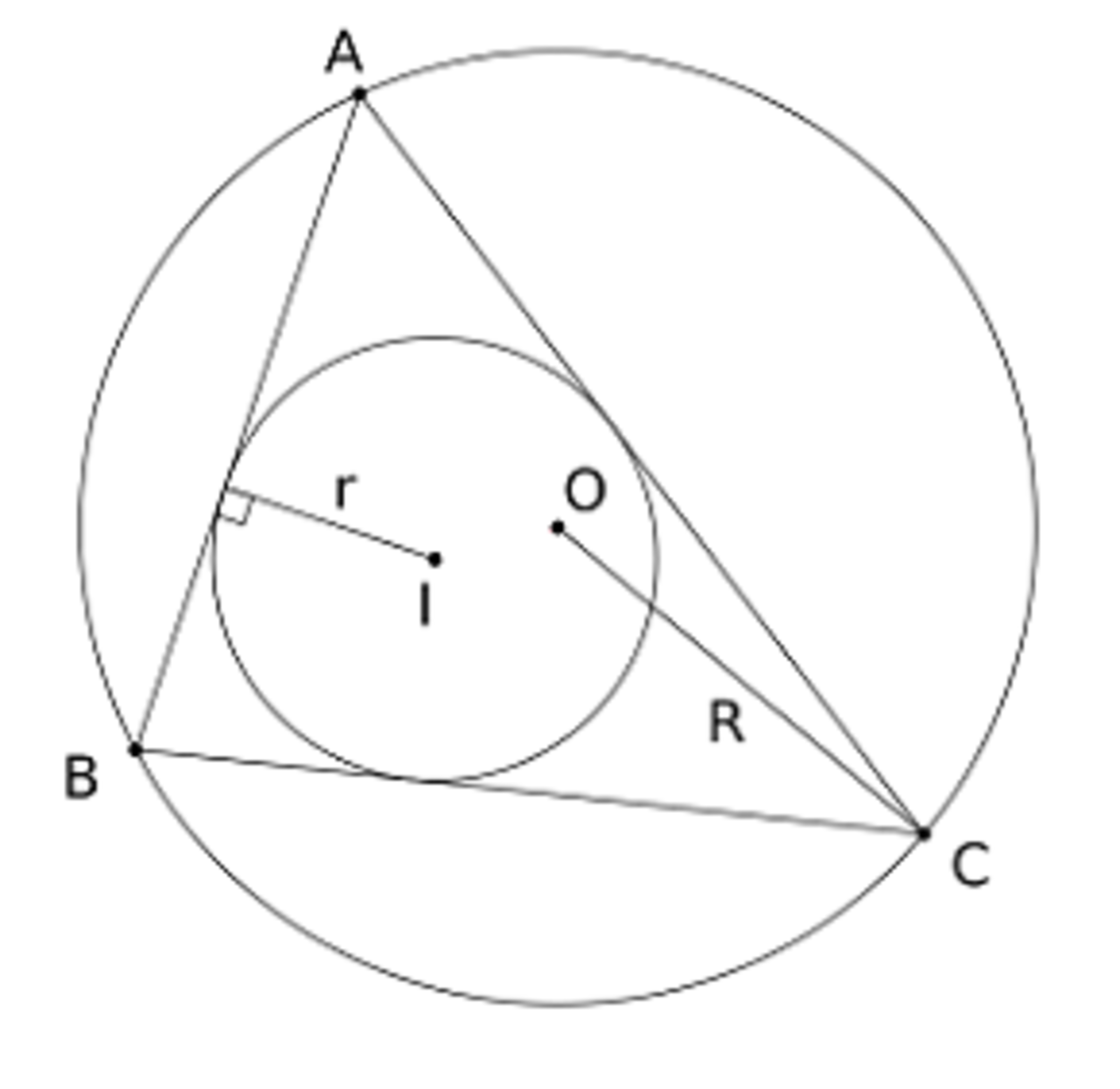
In △ A B C , let R and r be the circumradius and inradius respectively (the radii of the circumscribed circle and inscribed circle respectively).
Find the minimum value of r R .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let D be the second intersection of A I with the circumcircle ω of Δ A B C . We need to prove that 2 R r = R 2 − O I 2 = ∣ p o w ( I , ω ) ∣ = A I ⋅ I D . By Incenter-Excenter Lemma, we know D I = D B . So, we need to find similar triangles that contain the sides A I , B D , r and 2 R . Let E be the diametrically oppositie point of D on ω ; Thus E D = 2 R and ∠ E B D = 9 0 ∘ . Let F be the tangent point of incircle with side AB. Thus I F = r and ∠ I F A = 9 0 ∘ . Since ∠ F A I ≡ ∠ B A D = ∠ B E D , the right triangle Δ A I F and Δ E D B are similar. Therefore,
I F A I = D B E D
A I ⋅ I D = A I ⋅ E D = E D ⋅ I F = 2 R r
It is easy to deduce that R 2 − 2 R r ≥ 0 ⟹ R ≥ 2 r Equality occurs iff O = I e.g. Equilateral Triangle. And we are done.
The Euler's inequality tells us R ≥ 2 r , which holds with equality only for equilateral triangles, making the answer 2 .
According to Euler's theorem for a triangle , the distance between circumcenter O and incenter I is given by O I 2 = R ( R − 2 r ) . This implies that R ≥ 2 r . Therefore, the minimum r R = 2 .