Eye of the Wave
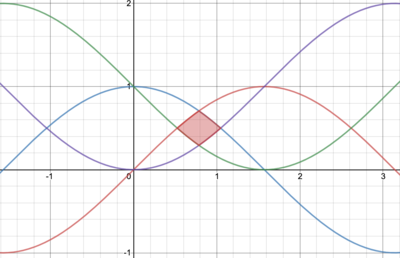
In the figure above, the red, blue, green, and purple curves represent , , , and respectively. The area of the shaded region can be expressed as , where and are square-free. Find .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is the x-coordinate of the intersection between the red and green lines is the solution to sin ( x ) = 1 − sin ( x ) , 0 ≤ x ≤ π , which is x = 6 π .
Using the same methods, we can find that the intersection between the blue and the red lines has an x-coordinate of 4 π , that between the purple and green lines 4 π , and that between the blue and purple lines 3 π .
As the shaded region is symmetric, it is double the area enclosed from x = 6 π to x = 4 π , which can be calculated by the integral of the red line minus the green line.
The shaded area is therefore
2 ∫ 6 π 4 π ( sin ( x ) − ( 1 − sin ( x ) ) ) d x
= 2 ∫ 6 π 4 π ( 2 sin ( x ) − 1 ) d x
= 2 [ − 2 cos ( x ) − x ] 6 π 4 π
= 2 ( − 2 2 3 − 6 π + 2 2 2 + 4 π )
= 2 ( 3 − 2 ) − 6 π
So A = 2 , B = 3 , C = 2 , D = 6 , giving the answer of 1 3 .