Magic of Math#2

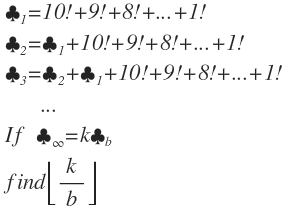
I have some questions about this question.

To start solving this question, I began by defining $\clubsuit_1\ = x$ , for purely simplification reasons. I then observed that:

$\clubsuit_1=x$

$\clubsuit_2=\clubsuit_1 + \clubsuit_1= 2\clubsuit_1$

$\clubsuit_3=\clubsuit_2 +\clubsuit_1 + x=\clubsuit_2+\clubsuit_2= 2\clubsuit_2$

$\vdots$

(1) $\clubsuit_n= 2\clubsuit_{n-1}$ , where n is a natural number s.t. $n \in (1, \infty)$

I then came to a metaphorical fork in the road. I was not certain whether the problem wanted (1) to be simplified in the form:

(2) $\clubsuit_n = 2^{n+1}\clubsuit_1$ , or not

Equation (2) can be obtained by observing the pattern of the equations obtained by substituting each occurrence of $\clubsuit_{n-1}$ with twice the previous term, ad infintum .

Although both (1) and (2) are equal, they would have very different conclusions as to the solution of the question. (1) would imply that:

$\lfloor \frac{k}{b} \rfloor =\lim_{b \to \infty} \lfloor \frac{2}{b} \rfloor = 0$ , which is the answer that was set as correct.

However (2) would imply that:

$\lfloor \frac{k}{b} \rfloor = \lim_{n \to \infty} \lfloor \frac{2^{n+1}}{n-1} \rfloor$ , which can be shown through the ratio test to be equal to $\lim_{k \to \infty} \lfloor k \rfloor = \infty$ . Therefore the answer to the question is $\infty$ . This answer is somewhat different.

I guess my main difficulty resides in the lack of specification of b. Is the question asking for b, s.t. b is a finite number or not?

If Diamond = X ('cause I can't type it :P) X(infinite)=(infinite-1)X(infinite) Floor k/b = Floor (infinie-1)/infinite = 0 Is that correct?