Facebook's 'People you may know' Feature Uses This Simple Algorithm
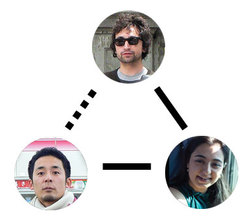 Ever wonder how Facebook suggests "People you may know"? One of the first (and simplest) algorithms that is used, is to look for strangers with whom you have many mutual friends.
Ever wonder how Facebook suggests "People you may know"? One of the first (and simplest) algorithms that is used, is to look for strangers with whom you have many mutual friends.
For example, if you and Colin are not friends on Facebook yet, but both of you are friends with Belinda, then {you, Belinda, Colin} form a Friend Suggestion Triangle (FST). The more FST's that exist, the more strangers Facebook can suggest with greater confidence that you might know them.
Out of a group of 10 people, what is the maximum number of FST's that exist?
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
Can you explain why each person can only be in 2 1 d i ( 9 − d i ) FSTs?
If there are 100 FSTs total, each of which contains 3 people, doesn't double counting combined with the pigeon hole principle tell us that there is some person that is in at least 30 FSTs?
Can you explain why each person can only be in 2 1 d i ( 9 − d i ) FSTs?
I was a bit unclear. First of all, I am counting the FSTs by the strangers in each FST. Each FST that has person i as one of the strangers has to contain one person she doesn't know ( d i choices) and one person she does know ( 9 − d i choices). Second, I neglected to point out that I was preemptively dividing the terms by two to account for that fact that each FST would enter the sum twice (once for the term of each of the two strangers in each FST). It would have been more appropriate to divide outside the sum. Finally, each person will appear in additional FSTs as the common friend.
If there are 100 FSTs total, each of which contains 3 people, doesn't double counting combined with the pigeon hole principle tell us that there is some person that is in at least 30 FSTs?
The language in my solution was more strict than I intended it to be. In the diagram I show, each person would be in d i ( 9 − d i ) = 2 0 unique groups as one of the strangers and in ( 2 5 ) = 1 0 unique groups as the common friend, making 30.
tl;dr: Yes!
In my three tries, I could not do it. But now I have understood. I will like to explain this in the following way: Let A, B, C, D, .....,J be the 10 persons. For A, the number of possible FSTs comes out to be 1 8 + 2 7 + 3 6 + 4 5 = 60 Thus, for all 10, it is 600. To avoid double counting, divide this by 3! Thus we get the answer 100
From your explanation ( Josh Silverman ), i didn't understand how double counting is explained.. A and B are friends, B and C are friends -- FST : A,B,C A and C are friends, B and C are friends -- FST : A,B,C A and B are friends, A and C are friends -- FST : A,B,C I think all are same..So how are maximum FSTs 100 ? Please provide further insight
Sorry Anoop, I didn't see this until now.
For each term in my sum, I am counting the number of FSTs for which that person (person i ) is the person who knows only one of the people in the FST. I divide this number by 2 since each FST will contain two such people.
I think it would be more transparent if we simply sum i ∑ d i ( 9 − d i ) and divide the whole sum by 2 at the end. Does that make things any more clear?
how abt this guys
I believe the maximum is 100. Divide the 10 people into 2 groups of 5. In each group, no one knows anyone else, but each of them knows every member of the other group. So each of the 10 people act as the 'primary vertex', (by which I mean the person who knows each of the other two in the FST), to C(5,2) = 10 FSTs. (The C(5,2) term comes from choosing 2 of the 5 people in the other group.)
Since there can only be one 'primary vertex' in any FST, each of these 10*10 = 100 FSTs will be unique.
Lets divide 10 in two groups group A and group B with 10 - x people and other with x people respectively. Each person in a group doesn't knows other members but knows all the members of the other group. Take any two member of a group A, the two don't know each other but they have all members of group B as common friends, so for two members we have x FSTs. Now there ( 2 1 0 − x ) such pairs of two in group A so x ( 2 1 0 − x ) FSTs for a group A. Similarly for group B we have ( 1 0 − x ) ( 2 x ) FSTs.
Total FSTs = x ( 2 1 0 − x ) + ( 1 0 − x ) ( 2 x ) = 4 x ( 1 0 − x ) Maximum of which occurs at x = 5 , which is 1 0 0 FSTs
Can you explain why this gives a maximum? Why does having these two groups give us the optimal solution?
To get maximum value, you can differentiate 4x(10-x) and equate it to 0 to get value of x as 5!!
4x(10-x) = 40x-4x^2
differentiating this and equating it to 0 , you will get, 40-8x=0
which gives x=5!!!!!
I think Lino means, how are you so sure that splitting is the best possible option? Not about the extreme value of 4x(10-x) .
Let me explain this with the case when x = 5, so we have 5 members in both groups and each person in a group doesn't knows other members but knows all the members of the other group. Now suppose a member of group A, A1, knows another member of group A, A2, doing this you destroyed 5 FSTs which are (A1, B1, A2), (A1, B2, A2) .... (A1, B5, A3). And if a member of group A, A1, doesn't knows a member of group B, B1, then also you destroyed 5 FSTs which are (A1, B1, A2), (A1, B1, A3) ... (A1, B1, A5). So doing and changes in the pattern of group will lead to more destruction than construction of FSTs, that's why these two groups gives us optimal solution.
I chose to take it step by step, starting from 4 people (maxfst(4) = 4)
if 4 people are named a, b, c, d, respectively, the configuration that maximises FSTs is when a is not friends with b and c is not friends with d
suppose a 5th person e comes into the picture. under the assumption that the maxFST(n) = maxFST(n-1) + number of FSTs that include the nth person (i.e. non-maximising configurations of (n-1) people cannot generate maximising configurations for n people), maximising the FSTs with 5 people is a matter of choosing who e is friends with.
if e is friends with a, let a = 1, otherwise a = 0, and the same applies to b, c, and d.
since a is not friends with b, e needs to be friends with both a and b to form the FST abe. since a is friends with c, e needs to be friends with exclusively either a OR c to form the FST ace.
this produces a series of logic gates, whose sum, when added to 4 (maximum FSTs with (n-1) people), is equal to the maximum FSTs with 5 people.
a AND b a XOR c a XOR d b XOR c b XOR d c AND d
the ordered quadruplet (a, b, c, d) = (1, 1, 0, 0) gives 9 FSTs with 5 people, 1 shy of the total number of triangles = ( 3 5 ) = 10. it is trivially proven that 10 is impossible; because of the AND gates; if both a AND b and c AND d are equal to 1, then all other 4 gates have to be 0; hence at least either one of the AND gates must be 0.
we repeat the process for the 6th person f, this time with 4 new logic gates: a XOR e, b XOR e, c AND e, d AND e. since the configuration used previously was (1, 1, 0, 0), f must be friends with either a or e (not both) to produce FST aef, but both c and e to produce cef.
paying attention to the AND gates since intuitively they are the most restrictive, maximising FSTs for 6 people is quite simply (0, 0, 1, 1, 1, 1); and when the results of the gates are summed up, we get 9; adding this to 9, we get 18.
the process is repeated again and again until we reach the 10th person j; along the way, the AND gates seem to form between restricted pools of people; after this step a, b, f have AND gates all with one another and c, d, e also all with one another. to satisfy all the other XOR gates that exist, it's only a matter of setting all the people in one pool to 1 and the other pool to 0; this gives maxFST (n) - maxFST(n-1) = ( 2 ( n − 1 ) ) − ( 2 k ) = (total number of gates) - (number of AND gates sacrificed by setting one pool to 0), where k is the number of individuals in the smaller pool.
maxFST (7) = 18 + 15 - 3 = 30, maxFST (8) = 30 + 21 - 3 = 48, maxFST (9) = 48 + 28 - 6 = 70, maxFST(10) = 70 + 36 - 6 = 1 0 0 .
Thankfully this solution requires basic intuition only...
Name persons as A,B....J. Fix a person (say A) Now A can be friends with n (out of 9 others) and strangers to (9-n) remaining. Why not apply symmetry (i.e. Let each person be friends with n others and strangers to 9-n others. Symmetry is the point at which no. of FSTs is maximum (Don't ask why))
Put n = 5 (5 friends and 4 strangers)
Say A is friends with BCDEF. G is friends with BCDEF ... J is friends with BCDEF
Now, Out of AGHIJ, choose any two (=10 ways) For each such pair, there are 5 FSTs. (=>50 FSTs counted)
Now, Out of BCDEF, choose any two (=10 ways) For each such pair, there are 5 FSTs. (=>50 FSTs counted)
total = 100
Each person has d i people in the group who they don't know. If every person who they don't know does know every person who they do know, then each person can partake in a maximum number of FSTs, given by 2 1 d i ( 9 − d i ) .
Ignoring possible constraints, the maximum possible number of FSTs is given by
i ∑ max 2 1 d i ( 9 − d i ) = 1 0 max 2 1 d i ( 9 − d i ) = 1 0 0
We now show that such an arrangement is possible (blue indicates a random person of interest):
The sum is maximized by an arrangement in which the 10 people are partitioned into two sets of equal size, each containing people who don't know people in their own set, but do know every person in the other set.
Note : d i = 5 also maximizes the sum but it is not possible to put each person in a group with 5 people who they don't know. It is also not possible to put some people into a group with 5 people who they don't know and put others into a group with 4 people who they don't know because the first group would have to contain 6 people.