Factorial Digits

Number Theory Level 4

How many digits are there in 2015!

The answer is 5786.

4 solutions

Jessica Wang
Oct 17, 2015

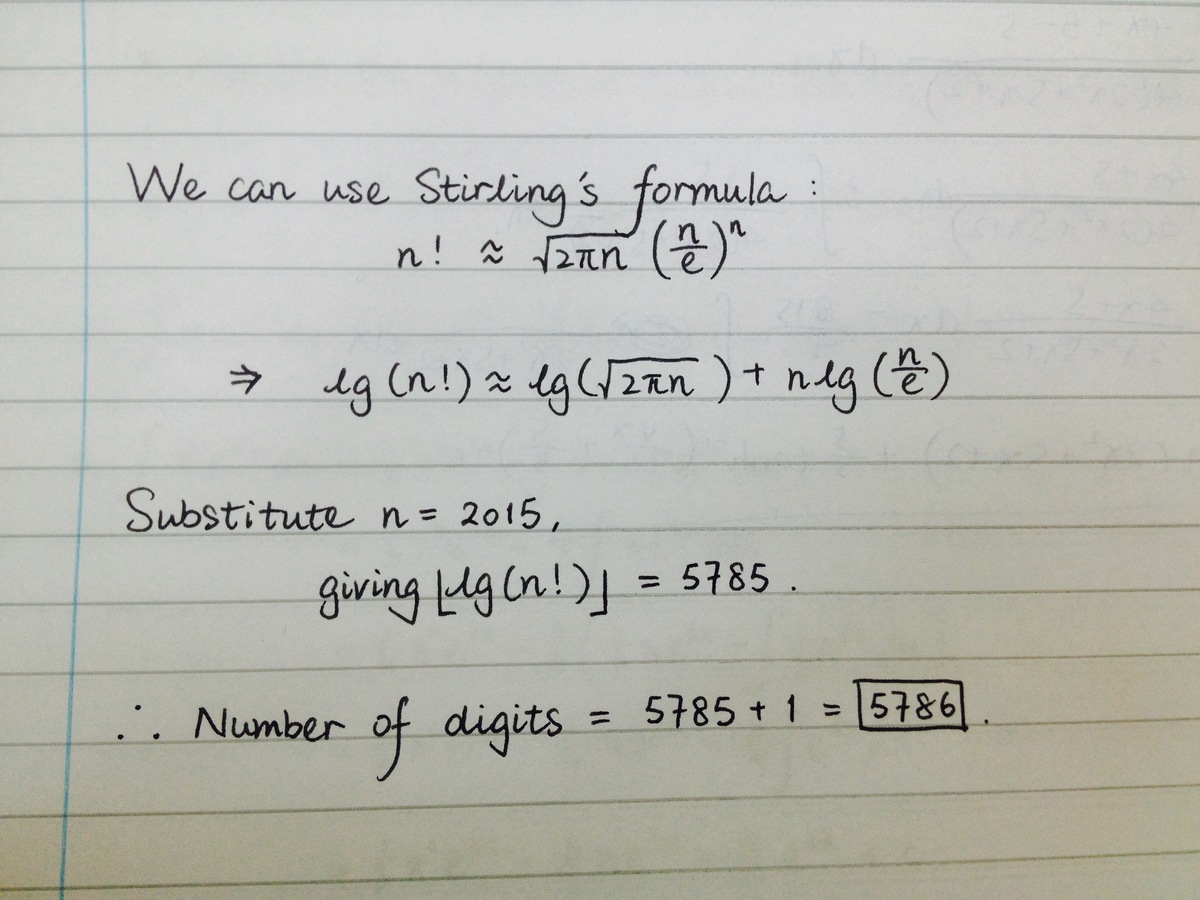
Why did you use the floor function first, then added +1 instead of using ceiling function from the beginning? Also the first few lines seem redundant to me, though I admit seeing Stirling's formula in action is always exciting.

Alisa Meier - 5 years, 8 months ago

Alisa Meier "Why did you use the floor function first, then added +1 instead of using ceiling function from the beginning?" -- Consider the situation where it is an integer. "Also the first few lines seem redundant to me [...]" -- For me , they are not redundant, as I think they help to explain the following steps. Moreover, a normal calculator cannot calculate $lg(2015!)$ directly.

P.S. You can always do this problem afterwards and also see the solution there.

Jessica Wang - 5 years, 8 months ago

@Jessica Wang

Moreover, a normal calculator cannot calculate $\text{lg}(2015!)$ directly.

Write as $\log(2015!) = \sum_{k=1}^{2015} \log k$ Though my calculator took five minutes just to evaluate that. XD

Jaydee Lucero - 3 years, 11 months ago

Ankit Nigam
Dec 27, 2015

I was not aware of stirling's formula before, so this helped me

#include <iostream>
#include <math.h>

using namespace std;

int main(){
    float s = 0;
    for(int i = 0; i<2015; i++){
        s += log10(i + 1);
    }
    cout << floor(s) + 1 << endl;
    return 0;
}

Ramiel To-ong
Oct 16, 2015

nice problem, just use Euler's Formula

How's that?

Ron Balter - 5 years, 8 months ago

There should be a way solving this via the Euler-Maclaurin formular. (my proof is yet incomplete)

Let $M$ be the numbers of digits we look for. Then we have $M = 1+ \lfloor {\frac{log \ (2015!)}{ log \ 10 }} \rfloor$

Problem is dealing with the $log(2015!)$

Now one can use Stirling's formular as done by @Jessica Wang

Or go via the Euler-Maclaurin formular: $\log(2015!) = \sum\limits_{k = 1}^{2015} \log(k) =$

$\int_{1}^{2015} \log(x) dx + \int_{1}^{2015} (x- \lfloor{x}\rfloor) \frac{1}{x} dx + \log(2015)( \lfloor 2015 \rfloor - 2015) - log(1) ( \lfloor 1 \rfloor - 1)$

$= (2015*\log(2015) - 2014) + (2014 - \int_{1}^{2015} \frac{\lfloor x \rfloor} {x}dx)$

At this point however I don't see a convenient dealing with the last integral. It would be nice to see this finished somehow.

Meer Kat - 5 years, 8 months ago

Ooh interesting extension Meer Kat $:P$

Jessica Wang - 5 years, 8 months ago

Jun Arro Estrella
Oct 19, 2015

Good work everyone.. I used stirling's formula..

Factorial Digits

The answer is 5786.

4 solutions

0 pending reports