Factorial of Quadratic Expression
Find the sum of all values of for the equation:
Clarification : The factorial in this problem is defined for integers (i.e. the Gamma function is not considered).
The answer is -10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
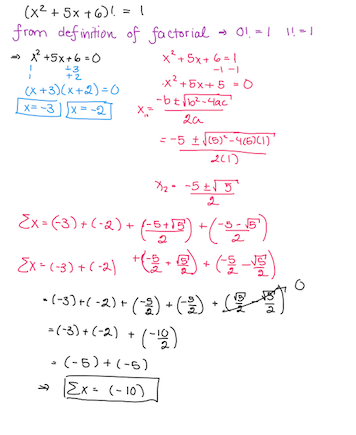
Solving y ! = 1
The solutions y = 1 and y = 0 are appearent by inspection. It is easily seen that there are no other positive solutions, as the factotrial increases uniformly over the positive integers.
Using only the integral solutions, we have x 2 + 5 x + 6 = 1 and x 2 + 5 x + 6 = 0 . By Vietas, the sum of the roots of both of these equations is − 1 0 .