Factorize the Box
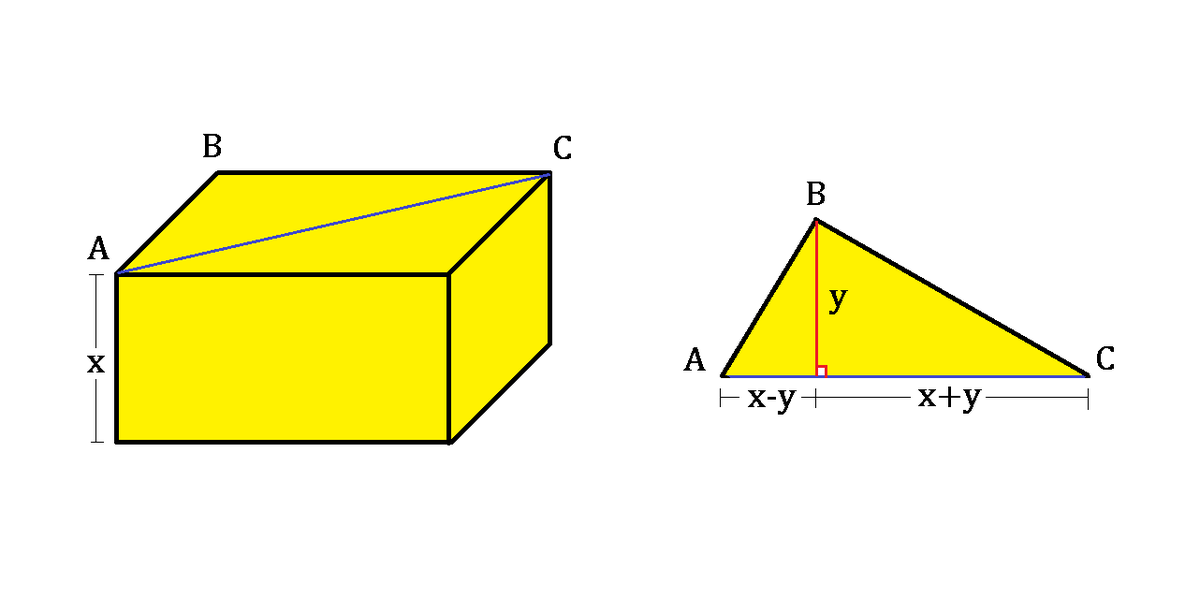
A cuboid box has a height of x and a base diagonal (in blue) of length 2 x .
Considering the triangle A B C separately, its height (in red) is y , partitioning the (blue) base into x − y and x + y , as shown above right.
If the volume of the box is 108, what is the value of y ?
Hint:
This
wiki
can help.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great use of Sophie Germain identity. It may not have striked me if you hadn't hinted the relevant wiki in the question!
Log in to reply
Thanks. I was trying to seek use of it. ;)
I ended up solving it without applying the identity in question. I was actually confused the entire time as I was progressing and just waiting to see when I would need the identity but I never did. Anyways, let's start. Let's say that the length of the segment AB is a and that the length of the segment BC is b. Then because the diagonal is 2x we know that a 2 + b 2 = 4 x 2 .
Now focusing on the triangle ABC we find that y 2 + ( x − y ) 2 = a 2 and y 2 + ( x + y ) 2 = b 2 . Now comes the crucial step. Let's add both sides to get y 2 + ( x − y ) 2 + y 2 + ( x + y ) 2 = a 2 + b 2 . We can now simplify the left side of this equality using simple algebra to get 4 y 2 + 2 x 2 . For the right side, we already know that it is equal to 4 x 2 so we have that 4 y 2 + 2 x 2 = 4 x 2 which yields 2 y 2 = x 2 and therefore y = 2 x . This is half the puzzle. Now to conclude I will rewrite the volume of the cube. We know that the volume of the cube is x a b but this is simply x times the area of the top face. And the top face is simply two times the area of the triangle ABC. So let's compute the area of the triangle ABC: 2 2 x y = x y = x 2 x = 2 x 2 . And the top face, which is two times this, is equal to 2 x 2 . Therefore the volume of the cube is 2 x 3 and to conclude we have the equality 2 x 3 = 1 0 8 which implies x 3 = 2 1 0 8 .
If we now cube the expression we had for y we get that y 3 = 2 2 x 3 . And plugging our value for x gives us y 3 = 4 1 0 8 = 2 7 and thus y = 3 .
Using the 2nd Euclid's Theorem (x-y)(x+y)=y^2 Thus x=y sqrt2 Volume=x 2x y sqrt2 Substituting 108=4y^3--->y=3
The area of the triangle is 2 1 × 2 x × y = x y .
Note that the cuboid has a base twice this area 2 x y , height x and hence volume V = 2 x 2 y .
Now study the triangle a bit closer.
Let's say D is the point where the perpendicular meets the line AC, and E is the midpoint of AC. Drawing a circle with center E and radius x, B must lie on the circle, since ABC is a right angled triangle. The right angled triangle EDB has two sides y and hypothenuse x so that x = y 2 , and we can write V = 1 0 8 = 2 ( y 2 ) 2 y = 4 y 3 ⇒ y = 3 4 1 0 8 = 3 .
Relevant wiki: Sophie Germain Identity
The base area of the cuboid = ( ( x − y ) 2 + y 2 ) ( ( x + y ) 2 + y 2 )
By using Sophie Germain Identity , we can apply:
x 4 + 4 y 4 = ( ( x − y ) 2 + y 2 ) ( ( x + y ) 2 + y 2 )
Hence, the base area = x 4 + 4 y 4
Now since the triangle A B C is a right triangle, and let B D be the red height, y x − y = x + y y because of similarity.
Then, x 2 − y 2 = y 2 .
x 2 = 2 y 2 or x = y 2 .
Therefore, the base area = x 4 + 4 y 4 = 4 y 4 + 4 y 4 = ( 2 2 ) y 2 .
Then, the cuboid's volume = ( 2 2 ) y 2 x = 4 y 3 = 1 0 8 .
As a result, y 3 = 2 7 . y = 3 .