Falling charges, how many will succeed?
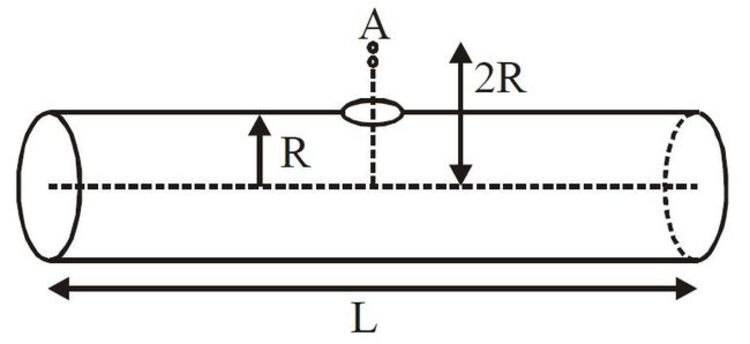 A horizontal conducting cylindrical hollow pipe of radius
and length
has a small hole
at its top, at the middle of the length as shown in the figure. Drops of mass
and charge
are falling into the hole from point
, at height
measured from the axis of the cylinder. Assume that the charge in the fallen drop gets uniformly distributed over the surface of the cylinder and charge distributed on cylinder remains uniform throughout. If the number of drops that will be able to enter the cylinder is given as
in scientific notation. Find the value of
.
A horizontal conducting cylindrical hollow pipe of radius
and length
has a small hole
at its top, at the middle of the length as shown in the figure. Drops of mass
and charge
are falling into the hole from point
, at height
measured from the axis of the cylinder. Assume that the charge in the fallen drop gets uniformly distributed over the surface of the cylinder and charge distributed on cylinder remains uniform throughout. If the number of drops that will be able to enter the cylinder is given as
in scientific notation. Find the value of
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Good question !
The exact answer is 9 . 7 9 × 1 0 3