Falling circle
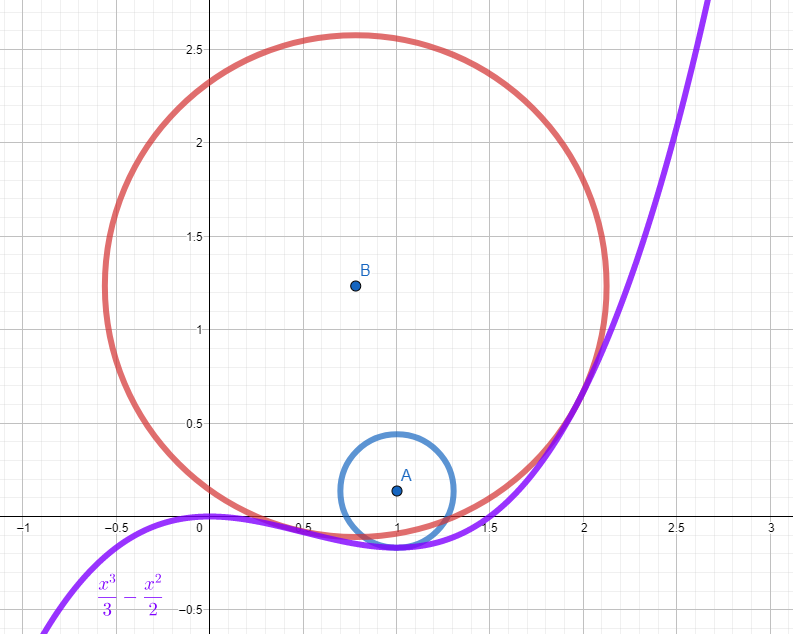
The small circle rests well in the local minimum of while the larger circle is forced up a bit but will still stay where it is.
What's the radius of the largest circle that won't roll away and down into the 3rd quadrant?
The answer is 2.52816185205477778.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The cubic equation has a local minimum at ( 0 , 0 ) . The largest circle will balance on this point and be tangent to the cubic at one other point (purple).
Let this other point be B = ( b , 3 b 3 − 2 b 2 ) and the slope at this point is the derivative b 2 − b , the perpendicular slope is b − b 2 1
The perpendicular line at this point is y − ( 3 b 3 − 2 b 2 ) = b − b 2 1 ( x − b )
which has y-intercept 1 − b − 1 + 3 b 3 − 2 b 2
The distance from B to this y-intercept must equal the y-intercept because both are the radius of the circle.
b 2 + ( 1 − b ) 2 1 = 1 − b − 1 + 3 b 3 − 2 b 2
This actually becomes a 10th-degree polynomial, the root we want comes from a cubic factor. But solving numerically, the solution of interest is b = 2 . 4 2 9 4 4 4 5 . . .
Plugging this into the y-intercept above gives the solution: 2 . 5 2 8 1 6 1 8 5 2 0 5 4 7 7 7 7 8 . . .