Falling Ladder
An 8 -ft ladder is leaning flat against a wall, when suddenly the base of the ladder slides away from the wall causing the top of the ladder to slide down the wall until the ladder is flat against the ground. Viewed from the side, the total area that is swept by the falling ladder can be expressed as n π ft 2 , where n is an integer. Find n .
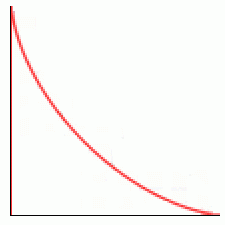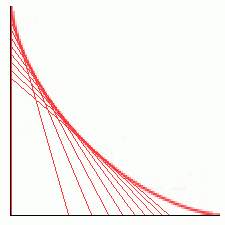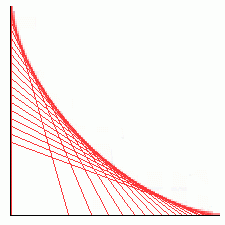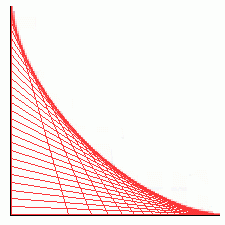
Assume that the ground and wall are perpendicular planes, and treat the ladder as a line segment with no width.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution, learned something new today!
A one typo and one, in my opinion, incorrect wording:
-
you've probably meant w cos θ − x y = w cos θ w sin θ .
-
"The maximum height y at any given θ is when d θ d y = 0 ...", put like this, sentence indicates that θ isn't the varying factor. At any given θ maximum height y naturally equals w sin θ . Better wording would be: "For fixed x , the maximum height y with respect to θ is when d θ d y = 0 . "
Log in to reply
Thank you! All of your suggestions were very helpful and I have edited my solution.
This is nearly identical to my "Squeegees" problem that I posted last year! Here is a link to that problem, which has a few relevant solutions...
You're right! I hadn't seen your squeegees problem before, but it's a good one.
by the picture one can recognize the astroid curve
Log in to reply
It is true that it is an astroid curve, but can you prove it without guessing from the picture?
Hi Miles Where's the link that you allude to?
Log in to reply
https://brilliant.org/problems/squeegees/?ref_id=1416869
Let the length of the ladder be w , the angle the ladder makes with the ground θ , and ( x , y ) be a coordinate on the ladder:
Then by similar triangles, w cos θ − x y = w cos θ w sin θ , which simplifies to y = w sin θ − x tan θ .
For a fixed x , the maximum height y with respect to θ is when d θ d y = 0 , so d θ d y = w cos θ − x sec 2 θ = 0 , which simplifies to cos θ = 3 8 x .
Then using the identities sin 2 θ + cos 2 θ = 1 and tan θ = cos θ sin θ we have y = w 1 − ( 3 8 x ) 2 − x 3 8 x 1 − ( 3 8 x ) 2 which can be rearranged to x 3 2 + y 3 2 = w 3 2 , which is the equation of an astroid .
Therefore, the area A swept by a falling 8 -ft ladder is the same as the area of an astroid in the first quadrant, which is A = 4 1 8 3 π 8 2 = 6 π , and so n = 6 .