Falling Pencil

As no energy is dissipated during the pencil's fall, we can find the equation of motion using the conservation of energy. The total energy is given by $E = \frac12 I\dot{\theta}^2 + \frac12 mgl\cos\theta$ Taking the time derivative we have $\begin{aligned} \dot{E} &= 0 \\ &=I\dot{\theta}\ddot{\theta} - \frac12mgl\sin\theta\dot{\theta} \\ &= I\ddot{\theta} - \frac12mgl\sin\theta \end{aligned}$ which yields the equation of motion $\ddot{\theta} = \frac{mgl}{2I}\sin\theta$ This relation is difficult to solve analytically so we can proceed by evaluating it numerically, or by making an approximation.

The differential relation we have to solve is very similar to the governing equation for the simple harmonic oscillator, where we can approximate $\sin\theta\approx\theta$ to analyze small oscillations. Here this might appear unwarranted since the pencil falls through the angle $\phi=\pi/2$ . However, as the pencil falls, it picks up speed, which means that it spends less time at the large angles. It is thus plausible that the time the pencil spends at small angles dominates the total time $T$ .

Let's therefore assume that the replacement $\sin\theta\rightarrow\theta$ is valid and proceed with caution. In this case we have $\begin{aligned} \ddot{\theta} &= \overbrace{\frac{mgl}{2I}}^{\omega^2}\theta \\ &= \omega^2 \theta \end{aligned}$ This has the solution $\theta(t) = \theta_0\cosh\omega t$ which predicts $T=\frac{1}{\omega}\cosh^{-1}\frac{\pi}{2\theta_0}$ or $T\approx\si{0.6574\ \second}$ for our system.

Below we plot the approximate analytic solution alongside the direct numerical integration of the exact differential equation. The numerical result yields $T\approx \si{0.6618\ \second}$ which is less than 1% off.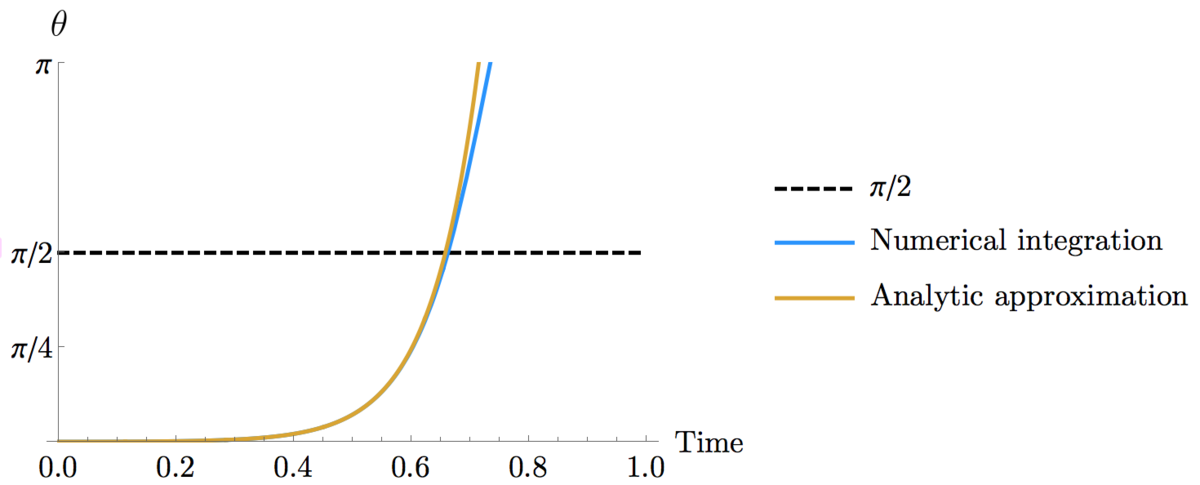

It would appear our approximation is quite good and that $T$ is dominated by motion through small angles.

Note: $I$ for our pencil is given by $\frac13 ml^2$ which we can see by summing up $r^2\delta m$ from the pivot to the end of the pencil $\displaystyle I = \int\limits_0^{l} r^2\, \delta m = \int\limits_0^{l} \frac{m}{l} r^2\, dr = \frac13 ml^2$