Familiar configuration

Geometry Level 3

Let $ABC$ be a triangle with area equal to $100$ , and $D, E$ are interior points of the sides $AB, AC$ , respectively.

Let $F$ be the intersecting point of $CD$ and $BE$ .

Find the maximum value of the area of triangle $DEF$ .

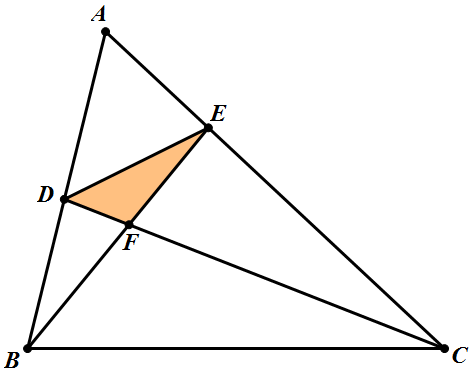
The answer is 9.017.

1 solution

Ivo Zerkov
Mar 19, 2018

If $\frac{\text{BD}}{\text{AB}}=a$ and $\frac{\text{CE}}{\text{AC}}=b$ , it’s fairly straightforward using Menelaus’ theorem to show $\text{DEF}$ ’s area to be $\frac{a\cdot b \cdot(1-a-b+a\cdot b)}{a+b-a\cdot b}$ of $\text{ABC}$ ’s. Maximizing this numerically yields $a=b\approx0.38197$ , making the answer $\approx9.017$ .

Familiar configuration

The answer is 9.017.

1 solution

0 pending reports