Family Of Circles
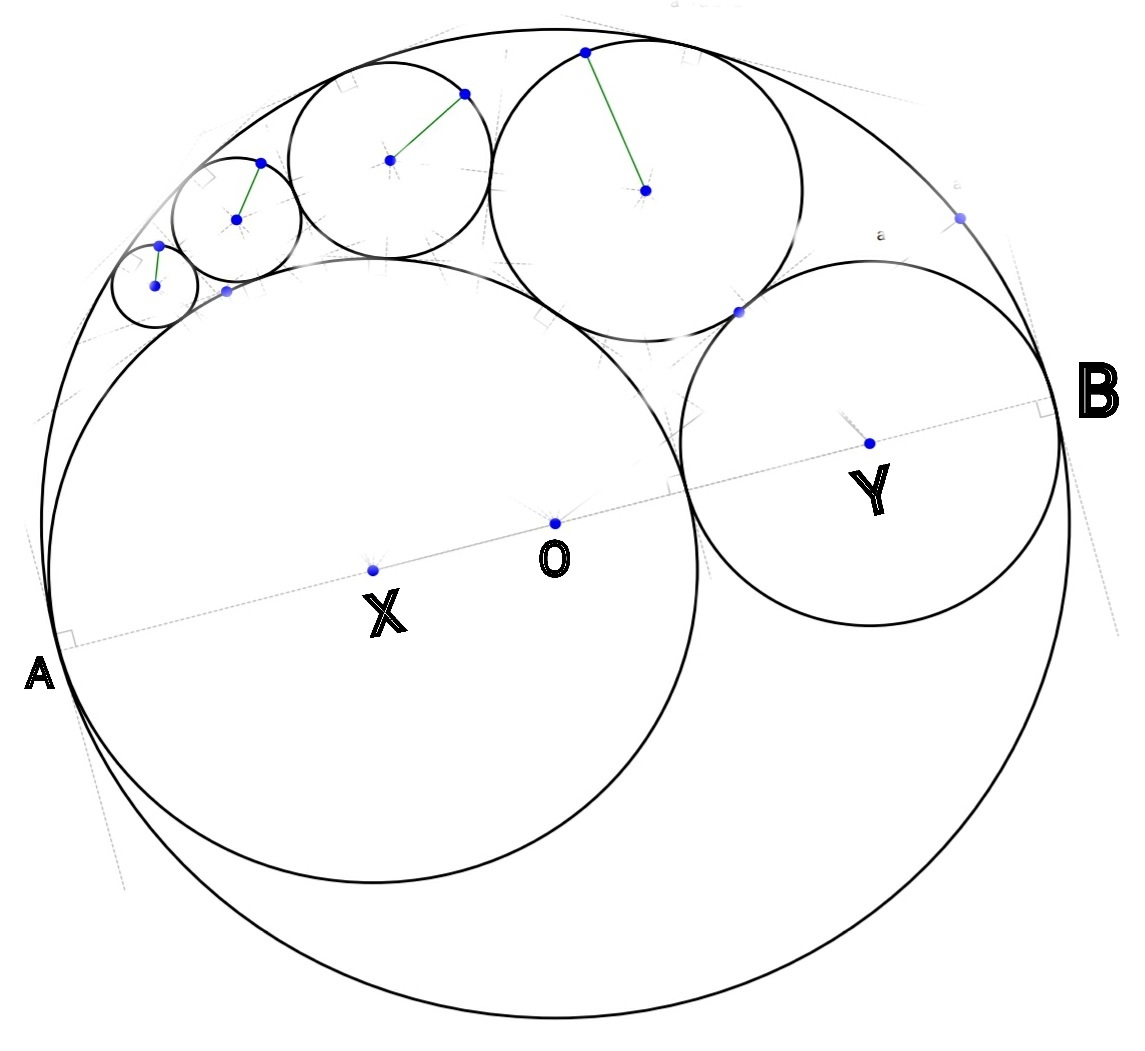
If A X = 2 and B Y = 1 , find the radius of the smallest circle to 2 decimal places.
The answer is 0.27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you explain how you went from the first equation to the second?
Log in to reply
2 k n + 1 k n + 2 1 k n + 1 + 2 1 k n 4 ( k n + 1 k n + 2 1 k n + 1 + 2 1 k n ) = k n + 1 + k n + 6 5 = ( k n + 1 + k n + 6 5 ) 2 Now solve this quadratic to find a positive k n + 1 in terms of k n .
- If the radius BY=a, AX =b
- The radius of larger circle is (a+b)
- Leaving these 3 circles, there is a generalised formula for calculating the radius of any circle tangent to these circles and the pattern continuing! The radius of nth circle is--
- ( a × b × ( a + b ) ) ÷ ( n 2 × a 2 + a × b + b 2 )
- so accordingly, radius of 4th circle in the pattern is-
- ( 1 × 2 × 3 ) / ( 1 6 × 1 + 2 + 4 ) = 0.272
- 0.27
Using your formula for a = 1 , b = 2 , n = 4 gives the answer of 1 1 3 ≈ 0 . 2 7 . You used it for a = 2 , b = 1 , n = 4 which gives the wrong answer.
Log in to reply
Ohh sorry I just pointed out, thanks @Maria Kozlowska
U s i n g D e s c a r t e s T h e o r e m , K 1 = − 1 / 3 , K 2 = 1 / 2 , K 3 = 1 / 1 . ∴ K 4 = − 1 / 3 + 1 / 2 + 1 / 1 ± 2 − 1 / 6 + 1 / 2 − 1 / 3 . G i v e s K 4 = 7 / 6 . F o r n e x t c i r c l e s , K 3 w i l l b e r e p l a c e d b y K n , a n d K 4 b y K n + 1 , n = 4 , 5 , 6 , 7 . S o K n + 1 = − 1 / 3 + 1 / 2 + K n ± 2 − 1 / 6 + 1 / 2 ∗ K n − 1 / 3 ∗ K n . ⟹ K n + 1 = 1 / 6 + K n ± 2 6 K n − 1 . n = 4 , K 5 = 1 / 6 + 7 / 6 ± 6 7 / 6 − 1 = 4 / 3 ± 1 / 3 . . . . . . . K 5 = 5 / 3 , K 3 = 1 / 1 . . ( c o r r e c t ) K 5 = 5 / 3 . n = 5 , K 6 = 1 / 6 + 5 / 3 ± 6 5 / 3 − 1 = 1 1 / 6 ± 2 / 3 . . . . . . K 6 = 5 / 2 , K 4 = 7 / 6 . . ( c o r r e c t ) K 6 = 5 / 2 . n = 6 , K 7 = 1 / 6 + 5 / 2 ± 6 5 / 2 − 1 = 8 / 3 ± 1 . . . . . . K 7 = 1 1 / 3 , K 4 = 5 / 3 . . ( c o r r e c t ) K 7 = 1 1 / 3 . R 7 = 0 . 2 7 2 7 2 7 .
Note that at every n t h circle we get two values. The - tive gives value of ( n − 1 ) t h circle, and that confirms with our previous value, tells us that our calculations are correct.
Not counting the circles of radius 3 and 2 , let k 0 , k 1 , k 2 , … , k 4 be the curvatures of the other circles. from largest to smallest. Then k 0 = 1 . For any 0 ≤ n ≤ 3 , we see that the circle of curvature 3 1 is externally tangent to the three mutually tangent circles of curvature 2 1 , k n and k n + 1 . Using Descartes Theorem, this implies that − 3 1 = k n + 1 + k n + 2 1 − 2 k n + 1 k n + 2 1 k n + 2 1 k n + 1 and hence that k n + 1 = 6 1 + k n + 3 1 6 ( k n − 1 ) A simple induction shows that k n = 6 1 ( 6 + n 2 ) 0 ≤ n ≤ 4 and hence k 4 = 3 1 1 , so the radius of the smallest circle is 1 1 3 = 0 . 2 ˙ 7 ˙ .