Fancy Quadrilateral
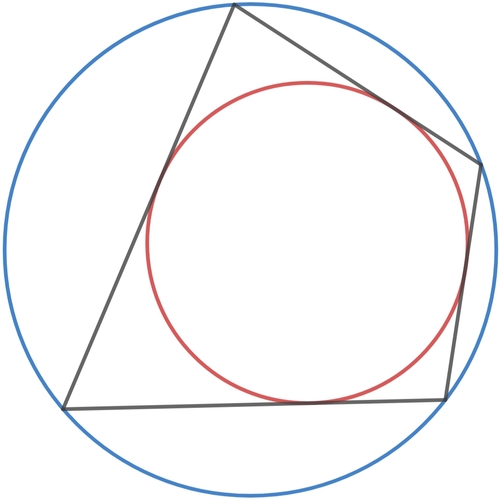
The figure shows the incircle and circumcircle of a given quadrilateral. The radii of the two circles are 7 and 1 2 .
If the distance between the centers of the two circles is x . Find x 2
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I also used Fuss' Theorem for solution. It is as under.
Here R=circumradius=12, and r=inradius=7, x=distance between centers.
x
2
=
R
2
+
r
2
−
r
4
R
2
−
r
2
=
1
2
2
+
7
2
−
7
4
∗
1
2
2
+
7
2
=
L
a
r
g
e
1
8
I didn't know about Fuss's Theorem, so I used a brute-force approach. I started with a circle of radius 12. Placed four point on it
with angular displacements (from the positive x-axis) of θ 1 , θ 2 , θ 3 , θ 4 .
I took θ 1 = 0 (fixed), and assumed that θ 1 < θ 2 < θ 3 < θ 4 .
The four vertices of the quadraliteral connecting these points on the circumference of the 12-radius
circle are P 1 , P 2 , P 3 and P 4 , where P i = 1 2 ( cos θ i , sin θ i ) .
Next I set up a Newton-Raphson multivariate iteration to find a solution for the required quadrilateral.
To have an incircle, it is required (by Pitot's theorem) that,
P 1 P 2 + P 3 P 4 = P 2 P 3 + P 4 P 1 = s , where s is the semi-perimeter, s = 2 1 ( P 1 P 2 + P 2 P 3 + P 3 P 4 + P 4 P 1 )
Next, for the current-iteration values of x 1 ( k ) = θ 2 ( k ) , x 2 ( k ) = θ 3 ( k ) , x 3 ( k ) θ 4 ( k ) , we can compute the
area of the quadrilateral, and thus compute a nominal (or average of some sort) inradius r , given by
r = s Area
So that the last equation to be satisifed is r = 7 .
Hence for the vector x ( k ) = [ x 1 ( k ) , x 2 ( k ) , x 3 ( k ) ] t , we define the problem as
follows:
F ( x ( k ) ) = 0
with
F 1 ( x ( k ) ) = P 1 P 2 + P 3 P 4 − s
F 2 ( x ( k ) ) = P 2 P 3 + P 4 P 1 − s
F 3 ( x ( k ) ) = r − 7
The Newton-Raphson iteration generates the next guess of x ( k ) as follows:
x ( k + 1 ) = x ( k ) − J − 1 ( x ( k ) ) F ( x ( k ) )
Where J ( x ( k ) ) is the Jacobian matrix for the vector function F ( x ( k ) ) ,
and is defined by J ( x ( k ) ) = [ J i j ] = [ ∂ x j ∂ F i ]
I found an approximation for the Jacobian matrix using numerical differentiation, then incorporated it in the iteration.
The Newton-Raphson method converged in 10 iterations. Having found the quadrilateral, what was left is simple
geometry to find the coordinates of the incenter, and this is easy to find by taking the intersection point of the
angle bisectors of two adjacent vertices. Finally, the square of the distance between the two centers is the sum of the
squares of the coordinates of the incenter.