Faraday generates electricity using rivers!
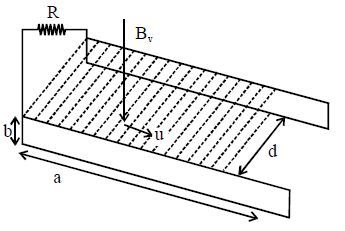 The figure shows an apparatus suggested by Faraday to generate electric current from a
flowing river. Two identical conducting plates of length
and width
are placed parallel facing one another on opposite sides of the river flowing with velocity
at a distance
apart. Now both the plates are connected by a load resistance
. Then the current through the load
is?
The figure shows an apparatus suggested by Faraday to generate electric current from a
flowing river. Two identical conducting plates of length
and width
are placed parallel facing one another on opposite sides of the river flowing with velocity
at a distance
apart. Now both the plates are connected by a load resistance
. Then the current through the load
is?
Consider vertical component of the magnetic field produced by earth is and the resistivity of river water is .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The river can be considered as large number of rods of length d connected in parallel.
Emf of each rod is B v u d since all rods are in parallel so the equivalent emf is B v u d the internal resistance of river is r e s i s t i v i t y × A r e a o f c r o s s − s e c t i o n l e n g t h
which is equal to a b ρ d
now current I = l o a d r e s i s t a n c e + i n t e r n a l r e s i s t a n c e E m f
SO the answer is I = R + a b ρ d B v u d