Faraday's drawings
Two charges
+
q
and
−
q
are separated by a distance
d
=
5
0
cm
. The electric field lines for this system form the the well-known pattern showed in the figure below.
Consider two lines
L
1
and
L
2
lying on the same plane and leaving the positive charge at
α
=
±
4
5
∘
.
What is the maximum distance
D
between the lines
in centimeters
.
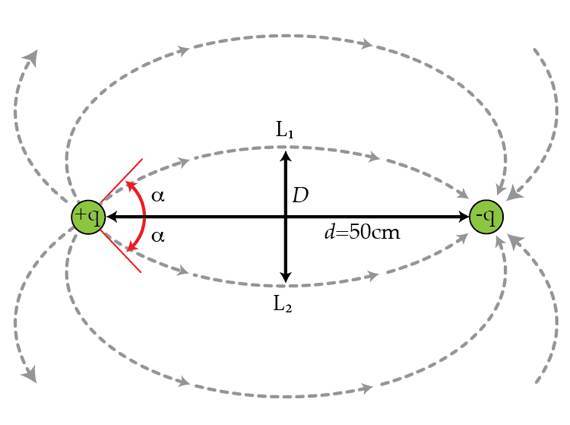
The answer is 30.52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Here is a simple argument based on solid angles.Considering the the field line any point on it is of the form c o s θ 1 + c o s θ 2 = c .Where c is a constant, θ i , i = 1 , 2 represents the angle made by the line joining the point and the ith charge.This is because through say a circular surface subtending the above said angles the flux remains constant as the no of field lines remains the same(rotstethe line to get a volume).So the sum of the subtends solid angles is a constant.Thereby the eq follows.The constant c is determined from initial conditions
Draw a disc emerging at an angle 45 from q {Larger disc}. Let e the be the permittivity of surroundings , and β be the angle subtended by the smaller disc to q {Whose diameter is L1L2}. Let the flux passing through larger disc in the absence of -q be N1. Let the flux passing through smaller disc be N2. Then N1=N2 q(1-Cos(45))/2e=q(1-Cosβ)/e hence Cosβ=.85360 L1L2=2 25 (Tanβ)=30.52cm
x is the distance from + q in the x direction, and y is the distance from + q in the y direction.
Because electric field lines are tangent to the electric field at all points, we can say d x d y = E x E y , where E y and E x are the x and y components of the electric field E due to the two charges.
To determine E y and E x , we must first determine the components of the two electric fields E + , E − due to the two charges that make up the total electric field E .
$$|\mathbf{E_+}|=\frac{kq}{r^2}=\frac{kq}{x^2+y^2}$$
$$\mathbf{E +}=|\mathbf{E +}|\langle \cos \theta, \sin \theta \rangle$$
where θ is the angle that E + makes with the x-axis.
$$\mathbf{E_+}=\frac{kq}{x^2+y^2}\langle \frac{x}{\sqrt{x^2+y^2}}, \frac{y}{\sqrt{x^2+y^2}} \rangle$$
$$=\langle \frac{kqx}{(x^2+y^2)^{3/2}},\frac{kqy}{(x^2+y^2)^{3/2}} \rangle $$
$$|\mathbf{E_-}|=\frac{kq}{(d-x)^2+y^2}$$
$$\mathbf{E_-}=\frac{kq}{(d-x)^2+y^2} \langle \cos \phi, -\sin \phi \rangle, $$
where ϕ is the angle E − makes with the negative x-axis.
$$\mathbf{E_-}=\frac{kq}{(d-x)^2+y^2} \langle \frac{d-x}{\sqrt{(d-x)^2+y^2}}, -\frac{y}{\sqrt{(d-x)^2+y^2}} \rangle $$
$$=\langle \frac{kq(d-x)}{((d-x)^2+y^2)^{3/2}},-\frac{kqy}{((d-x)^2+y^2)^{3/2}} \rangle$$
$$\mathbf{E}=\mathbf{E +} + \mathbf{E -}$$
$$E x = E {+,x} + E_{-,x}$$
$$E_x=\frac{kqx}{(x^2+y^2)^{3/2}} +\frac{kq(d-x)}{((d-x)^2+y^2)^{3/2}} $$
$$E y = E {+,y} + E_{-,y}$$
$$E_y=\frac{kqy}{(x^2+y^2)^{3/2}}-\frac{kqy}{((d-x)^2+y^2)^{3/2}}$$
$$\frac{dy}{dx}=\frac{E y}{E x}=\frac{\frac{y}{(x^2+y^2)^{3/2}}-\frac{y}{((d-x)^2+y^2)^{3/2}}}{\frac{x}{(x^2+y^2)^{3/2}} +\frac{d-x}{((d-x)^2+y^2)^{3/2}}}$$
Using numerical methods to solve this differential equation with initial condition y ( 1 0 − 3 c m ) = 1 0 − 3 c m (This is to approximate the field line leaving the charge at an angle of 45 \deg) yields y ( 2 5 c m ) = 1 5 . 2 6 c m . By symmetry we know that the maximum value of D will occur at x = 2 5 c m , and that it will be twice the height of the field line L 1 at that point.
$$D=2 \cdot y(25 \ \mathrm{cm})=30.52 \ \mathrm{cm}.$$
Could you please elaborate on how to solve the differential.
It is clear that the distance between the lines will be maximal at the point C which is equidistant from + q and − q . Let us consider the following Gaussian surface: Take the electric field line L 1 going from A to C , rotate it about the x-axis and remove a small spherical sectors with angle α as shown in the figure. Note that the electric flux through this surface must be zero as it does not enclose any charges. Let us determine the flux through the spherical cap 1. Since the sector is small, the mean contribution to the flux comes from the charge + q (the field is very strong in the vicinity of a point charge). We can write Φ 1 = E 1 A 1 = k R 1 2 q = k R 1 2 q 4 π R 1 2 sin 2 ( 2 α ) = ϵ 0 q sin 2 ( 2 α ) . Here, we have used the formula for the area of the spherical cap A = 4 π R 2 sin 2 ( 2 α ) . Thus, we have found that the flux through the spherical cap 1 is simply given by Φ 1 = ϵ 0 q sin 2 ( 2 α ) . Now we need to determine the flux through the disk (at x = 0 ) which closes the Gaussian surface. This flux equals The electric field is always in the x-direction at x = 0 and its magnitude is given by Coulomb's law + a little geometry,
E x = 8 π ϵ 0 q ( 0 . 2 5 2 + y 2 ) − 3 / 2 .
We can straightforwardly integrate this electric field over the disk to get the flux Φ 2 ,
Φ 2 = 8 π ϵ 0 q ∫ 0 D / 2 ( 0 . 2 5 2 + y 2 ) 3 / 2 2 π y d y .
Setting Φ 2 = Φ 1 yields D = 3 0 . 5 2 c m .
We can solve this one. like all other of this kind, by observing that the equation of a field line is q cos θ 1 − q cos θ 2 = c for a constant c , where θ 1 , θ 2 are the angles made with the line joining the two charges by the lines from a point in the plane to the charges of q , − q respectively.
In the case of the "upper" of the two fields lines of interest, when the field line leaves the q charge we have θ 1 = 4 1 π and θ 2 = π , which tells us that q c = 1 + 2 1 . This is consistent with what happens when the field line enters the − q charge; by symmetry we have θ 1 = 0 and θ 2 = 4 3 π there.
This fieldline's maximum deviation from the centre line will occur in the middle, when θ 1 = θ and θ 2 = π − θ . At that point we have 2 cos θ = cos θ 1 − cos θ 2 = 1 + 2 1 , so that tan θ = 2 3 − 1 6 2 . The distance D we want is D = 2 × 2 1 d tan θ = 5 0 2 3 − 1 6 2 = 3 0 . 5 1 9 7 8 8 7 5 cm.
consider a cone with its circular base at the mid pt of two charges (semi apex angle 45 degree ) and its end at +q
The net Flux through it due to +q (ignore -q)=
2 ( e ) q (1-cos45))**
now let us see the net electric field lines we find that net field comming due to net lines coming from the +q in presence of -q , we find that it form a smaller disc at the base of cone now we find the net flux through that small disc let it subtend a cone with semi apex angle theta
so net flux=
2 2 ( e ) q (1-cos(theta)**)
now since both are equal because gauss law says that flux is proportional to charge enclosed which is same so equating them
2 ( e ) q (1-cos45)) =2 2 ( e ) q (1-cos(theta) )
cos(theta)={sqrt(2)+1}/sqrt(8) but tan(theta)=(D/2)/(d/2)
N O T E −
(1)there is net electric flux through the closed surface then some electric field lines either originate or terminate within the volume enclosed.
(2) If no electric field lines originate or terminate within the volume enclosed, all of the field lines entering the volume exit the volume and there is thus zero net electric flux through the closed surface.
or simply we conclude that net flux contributed due to the fields that enter and exit a closed body =0.
it is q/2e(1-cos(theta)) not q/4(pi)e(1-cos(theta))
Log in to reply
yep sorry i will edit it .
i hope its fine now i forgot to multiply with 2pi while taking solid angle.
We use Gauss's law for the closed surface obtained by rotating left half of line L 1 and upper half of line D about the line d . There is non-zero flux only in the circular part of the surface ( circle A ) which can be calculated easily.So we have: Φ E = ϵ 0 q ′ ( ⋆ ) Where q ′ = f × q and f = Volume fraction of positive charge that lies inside the closed surface f = 3 4 π R 3 3 2 π R 3 ( 1 − cos α ) = 2 1 ( 1 − 2 2 ) Now we calculate Φ E : Φ E = ∫ A E . n ^ d A = ∫ 0 D / 2 E 2 π y d y Where y is the distance from the center of the circle A E = 2 r 2 k q cos θ = 2 4 d 2 + y 2 k q 4 d 2 + y 2 f r a c d 2 = ( 4 d 2 + y 2 ) 3 / 2 k q d which gives Φ E = ∫ 0 D / 2 ( 4 d 2 + y 2 ) 3 / 2 k q d 2 π y d y = 4 π k q d ( d 1 − d 2 + D 2 1 ) Finally from ( ⋆ ) 4 π 4 π ϵ 0 1 q d ( d 1 − d 2 + D 2 1 ) = 2 1 ( 1 − 2 2 ) ϵ 0 q d 2 + D 2 d = 2 1 + 4 2 we have d = 5 0 cm which gives D = 3 0 . 5 1 9 8 cm