Farmer Ram Hens

There are $92$ days total in the months of June, July, and August.

$Hen_{1}=1 \times92=92$

$Hen_{2}=(1+0) \times \frac{92}{2}=46$

$Hen_{3}=((1+0+0) \times \lfloor \frac{92}{3} \rfloor) + (1+0)=31$

$Hen_{4}=(1+0+0+0) \times \frac{92}{4}=23$

$Hen_{5}=((1+0+0+1+0+0+0) \times \lfloor \frac{92}{7} \rfloor) + (1)=27$

$Hen_{6}=((1+0+0+1+0+0+0+1+0+0+0+0) \times \lfloor \frac{92}{12} \rfloor) + (1+0+0+1+0+0+0+1)=24$

$92+46+31+23+27+24=243$

There are 30 + 31 + 31 = 92 days in the months June, July and August.

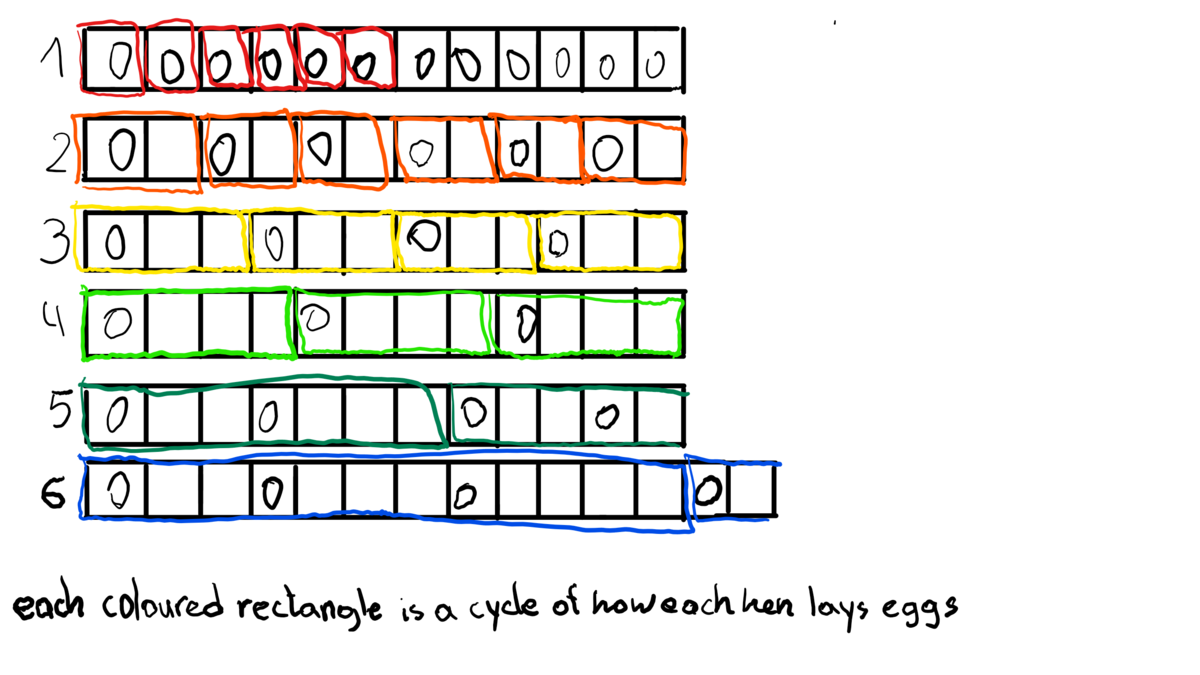
The first one lays 92 : 1(day in one cycle) = 92 full cycles 92 * 1(egg in one cycle) = 92 eggs

The second one lays 92 : 2(days in one cycle) = 46 full cycles 46 * 1(egg in one cycle) = 46 eggs

The third one lays 92 : 3(days in one cycle) = 30 full cycles and 2 days left which cover additional 1 egg 30 * 1(egg in one cycle) + 1 = 31 eggs

The fourth one lays 92 : 4(days in one cycle) = 23 full cycles 23 * 1(egg in one cycle) = 23 eggs

The fifth one lays 92 : 7(days in one cycle) = 13 full cycles and 1 day left which cover additional 1 egg 13 * 2(eggs in one cycle) + 1 = 27 eggs

The sixth one lays 92 : 12(days in one cycle) = 7 full cycles and 8 days left which cover additional 3 eggs 7 * 3(eggs in one cycle) + 3 = 24 eggs

92 + 46 + 31 + 23 + 27 + 24 = 243 total eggs from the six hens

Let us define an egg-laying function $e(n)$ for the number of eggs laid in $n$ days. For simple egg-laying cycle or period of 1, 2, 3, 4 ... $p$ days such as those for the first four hens, assuming an egg is laid on the first day of the cycle, we have $e(n) = \left \lceil \dfrac np \right \rceil$ , where $\lceil \cdot \rceil$ denotes the ceiling function . For the fifth hen, the egg-laying function is slightly modified to $e_5 (n) = \left \lceil \dfrac n7 \right \rceil + \left \lceil \dfrac {n-3}7 \right \rceil$ . Similar for the sixth hen, $e_6 (n) = \left \lceil \dfrac n{12} \right \rceil + \left \lceil \dfrac {n-3}{12} \right \rceil + \left \lceil \dfrac {n-7}{12} \right \rceil$ . Therefore, for the all six hens:

$\begin{aligned} e_{\text{6 hens}}(n) & = e_1(n) + e_2(n) + e_3(n) + e_4(n) + e_5(n) + e_6(n) \\ & = \left \lceil \frac n1 \right \rceil + \left \lceil \frac n2 \right \rceil + \left \lceil \frac n3 \right \rceil + \left \lceil \frac n4 \right \rceil + \left \lceil \frac n7 \right \rceil + \left \lceil \frac {n-3}7 \right \rceil + \left \lceil \frac n{12} \right \rceil + \left \lceil \frac {n-3}{12} \right \rceil + \left \lceil \frac {n-7}{12} \right \rceil \end{aligned}$

For $n=92$ :

$\begin{aligned} e_{\text{6 hens}}(92) & = \left \lceil \frac {92}1 \right \rceil + \left \lceil \frac {92}2 \right \rceil + \left \lceil \frac {92}3 \right \rceil + \left \lceil \frac {92}4 \right \rceil + \left \lceil \frac {92}7 \right \rceil + \left \lceil \frac {{92}-3}7 \right \rceil + \left \lceil \frac {92}{12} \right \rceil + \left \lceil \frac {{92}-3}{12} \right \rceil + \left \lceil \frac {{92}-7}{12} \right \rceil \\ & = 92 + 46 + 31 + 23 + 14 + 13 + 8 + 8 + 8 \\ & = \boxed{243} \end{aligned}$