Fast-moving wires
Consider two long parallel wires with linear charge density λ (charge per unit length) separated by a distance d. The wires move in the same direction (parallel to the wire direction) at a constant speed v. For what value v in meters per second the magnetic attraction balances the electrical repulsion? You do not need special relativity in order to solve the problem correctly. Note that even though the charge density is frame dependent, the choice of the frame does not affect the answer.
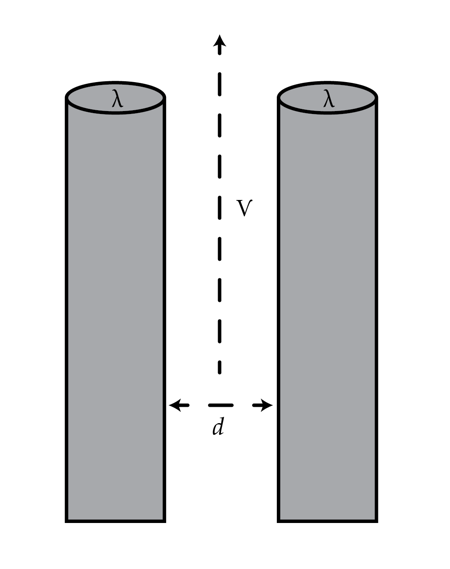
Details and assumptions
ϵ 0 = 8 . 8 5 × 1 0 − 1 2 F / m 4 π μ 0 = 1 0 − 7 H / m
The answer is 2.99863E+8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
first we need to visualize the motion of the cylinders as an equivalent of a current carrying conductor.The current is given by (lambda)dx/dt=(lambda)(v).magnetic field a distance of 'd' from the axis of a long current carrying wire is (mu)i/2(pi)d{by amperes law}.Consider an electron in the bulk of the other cylinder to be a test charge.Thus mag force on the electron is ev*B=ev[(mu)i/2(pi)d].The electric field E= [(lambda)/2(pi)(epsilon)d] {By gauss law}.So electrostatic force =eE. Equalizing both forced we get value of 'v'
Gauss' Law ∇ ⋅ E = ϵ 0 ρ applied to a cylinder of length L around one of the wires gives the electric field due to that wire.
Integrating over the volume L r 2 and applying the divergence theorem gives: E A = ϵ 0 λ L , where A = 2 π r L so E = 2 π ϵ 0 r λ
A similar procedure with Ampere's Law ∇ × B = μ 0 J gives the magnetic field due to a current I in a long straight wire as B = 2 π r μ 0 I . In this case the moving wire looks like a current so I = λ v .
We want to zero the Lorentz force F = q E + q ( v × B ) on any given segment of a wire. This can be done by setting the magnitudes E = v B . The right-hand rule of cross products ensures that the forces due to E and B will be in opposite directions- like charges repel but parallel currents attract.
Combining results from above: 2 π ϵ 0 r λ = v 2 π r μ 0 λ v . So v 2 = ϵ 0 μ 0 1 which means v = c = 3 . 0 0 × 1 0 8
A much faster route to the same result is to use the note that the 'choice of frame does not affect the answer.' c is the only invariant velocity.
In this issue, we must first calculate the electric and magnetic field created by each wire. The electric field is calculated by the Gauss's Law. Taking the Gaussian surface of a cylinder of radius d and height L , centered on one of the wires, we have: [; \phi = \frac {q}{\epsilon 0} = \frac { \lambda . L}{\epsilon 0} ;] We also have, in superfíicie the field is parallel to normal at each point. therefore: [;\phi = E.A = E.2.\pi.d.L;] Then: [; E = \frac {\lambda}{2.\pi.d .\epsilon 0};] Now, the magnetic field: [;B = \frac { \mu 0.i}{2.\pi.d} = \frac { \mu 0.\lambda.V}{2.\pi.d};] The value of i is because: [; i = \frac {\Delta q}{\Delta t} = \frac {\lambda . \Delta L}{\Delta t} = \lambda.V ;] Now, realizing that electrical forces are repulsive and the magnetic are attractive , simply equalize in module: [;Fm = B.i.l = \frac { \mu.i^2.l}{2.\pi.d} = \frac { \mu 0.\lambda^2.V^2.l}{2.\pi.d} ;] [;Fe = q.E = \frac {\lambda^2.l}{2.\pi.d .\epsilon 0} ;] Where l is any lenght of the both wires. Finally: [;Fe = Fm \rightarrow \frac {\lambda^2.l}{2.\pi.d .\epsilon 0} = \frac { \mu 0.\lambda^2.V^2.l}{2.\pi.d};] [;V = \frac {1} {\sqrt{\epsilon 0.\mu_0}} = c;] Where c is the speed of light by the maxwell's equation concatenation. [; c = 2.99.10^8 m/s;]
In each time t , each wire moves a distance l = v t , so the charge passing through each point is Q = λ l = λ v t . Thus, the current through each wire is I = t Q = λ v .
The magnetic force per unit length between two wires is l F = 2 π d μ 0 I 1 I 2 , so the magnetic force per unit length between the two moving wires is l F = 2 π d μ 0 λ 2 v 2 .
The electric field at one wire due to the other wire is E = 2 π ϵ 0 d λ . The electric force per unit length between the two wires is l F = l q E = λ E = 2 π ϵ 0 d λ 2 .
Equating the two forces and solving for v , we get v = ϵ 0 μ 0 1 . This is the speed of light c = 3 . 0 0 × 1 0 8 m / s .
From the Lorentz Force Law, when the forces balance, we have:
q E + q v B = 0
and from the wave equation, we know
∂ t 2 ∂ 2 E − c 2 ∇ 2 E = 0 and ∂ t 2 ∂ 2 B − c 2 ∇ 2 B = 0
Plugging in v B for E in the wave equation in the z-direction, we can solve:
∂ t 2 ∂ 2 v B − c 2 ∂ z 2 ∂ 2 E = 0
v ∂ t 2 ∂ 2 B − c 2 ∂ z 2 ∂ 2 E = 0
v ( v ∂ z 2 ∂ 2 E ) − c 2 ∂ z 2 ∂ 2 E = 0
v 2 ∂ z 2 ∂ 2 E − c 2 ∂ z 2 ∂ 2 E = 0
v = c
Let us first compute the electric force per unit length. This can be done by finding the electric field produced by one wire and multiplying the result by
λ
. The electric field produced by an infinite line charge can be easily determined from Gauss's Law. Taking a cylindrical Gaussian surface or radius r and height h we obtain
E
(
r
)
2
π
r
h
=
ϵ
0
q
→
E
(
d
)
=
2
π
ϵ
0
d
λ
.
So, both wires experience an external electric field of intensity
E
(
d
)
and a repulsive electric force per unit length
F
e
=
2
π
ϵ
0
d
λ
2
.
The magnetic force can be found in a similar fashion. First we notice that the motion of the charges implies the electric current
I
=
Δ
t
Δ
Q
=
λ
Δ
t
Δ
l
=
λ
v
.
From Ampere's Law we now find that the magnetic field produce by one wire is
B
=
2
π
d
μ
0
I
=
2
π
d
μ
0
λ
v
.
The magnetic force acting on a conductor of length L carrying a current I is given by the familiar formula
F
=
I
B
L
.
Therefore, the attractive magnetic force per unit length equals
F
m
=
2
π
d
μ
0
I
=
2
π
d
μ
0
(
λ
v
)
2
.
Setting
F
e
=
F
m
we obtain
v
=
ϵ
0
μ
0
1
,
that is, the speed of light!
Note that we didn't have to use special relativity to solve the problem. The above charge density
λ
is measured in the laboratory frame.
Isn't this obvious that we did not have to use special relativity. Though SR gives us the correct explanation but Magnetism is nothing but special relativity combined with electrostatics and is mathematically more simpler to use.
The electric field of a long wire is approximately E = 2 π r ϵ 0 λ . If L is the length of the wire, the force one wire exerts on the other is F e = charge * E --> F e = 2 π r ϵ 0 λ 2 L because charge = λ L .
The magnetic force can be calculated using F m = 2 π r μ 0 I 1 I 2 L , where I 1 and I 2 are the currents in wires 1 and 2, respectively. We can arrive at expressions for these currents if we remember that current is defined as charge per unit time passing through a surface. Let d be some distance traveled by the wires in time t. Then, we have I 1 = I 2 = t i m e c h a r g e = v d λ d = λ v .
Substituting this into our expression for the magnetic force gives F m = 2 π r μ 0 λ 2 v 2 L .
Now we just need to equate the electric and magnetic forces. We get:
2 π r ϵ 0 λ 2 L = 2 π r μ 0 λ 2 v 2 L
A bunch of stuff cancels, and we're left with v = ϵ 0 μ 0 1 .
This is easily recognizable as the expression for the speed of light, and evaluates to approximately 299863000 m/s, which is our answer.