Fastest checkmate 3

Logic Level 2

In the position below, how can White give the fastest checkmate?

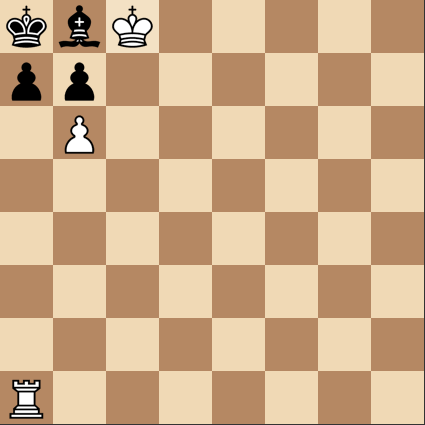
The target square of the last move can be represented as a coordinate ∖((x,y)∖), where the bottom left corner is at ∖((0,0)∖). Input ∖(y∖) as your answer.

The answer is 6.

2 solutions

A Former Brilliant Member
Feb 24, 2016

@Alexander Katz There are two possibilities. Ra6(0,5) bxa6(0,5) b7(1,6)# or Ra6(0,5) Bishop moves anywhere and Rxa7#(0,6). It took my two tries to get this question right. Please edit the question.

[EDITOR NOTE: Ra6 does not force a bishop move. Black can now move the pawn at a7 and then slow things down (there's still a mate in 8, but that's clearly not the fastest checkmate.]

I think you meant Ra6 (0,5) as the first move.

I only considered Ra2 (or Ra3, Ra4, etc.) waiting for the bishop to move.

You made a good point that another possibility exists.

Steven Perkins - 5 years, 3 months ago

Yes that is what I meant thanks for pointing it out.

There is indeed another possibility and I am surprised that a moderator has not edited the question yet. I have posted a report to the problem now.

A Former Brilliant Member - 5 years, 3 months ago

That is the reason why the $y$ coordinate is asked because regardless of which move black makes, the check will occur in the same row.

Rishik Jain - 5 years, 2 months ago

Just a side note, but to reach THAT far into the game, pretty sure it isn't the fastest checkmate.

Jase Jason - 5 years, 3 months ago

I'm not sure I know what you mean, but this problem is to determine the fastest checkmate starting from the given position.

Steven Perkins - 5 years, 2 months ago

A Former Brilliant Member
Mar 7, 2018

The last move for white can be Rxa7# or b7#. They are on the same rank (rank 7). So the desired answer is 6 since we start from zero in the first rank.

Fastest checkmate 3

The answer is 6.

2 solutions

0 pending reports