Fault Locator Error

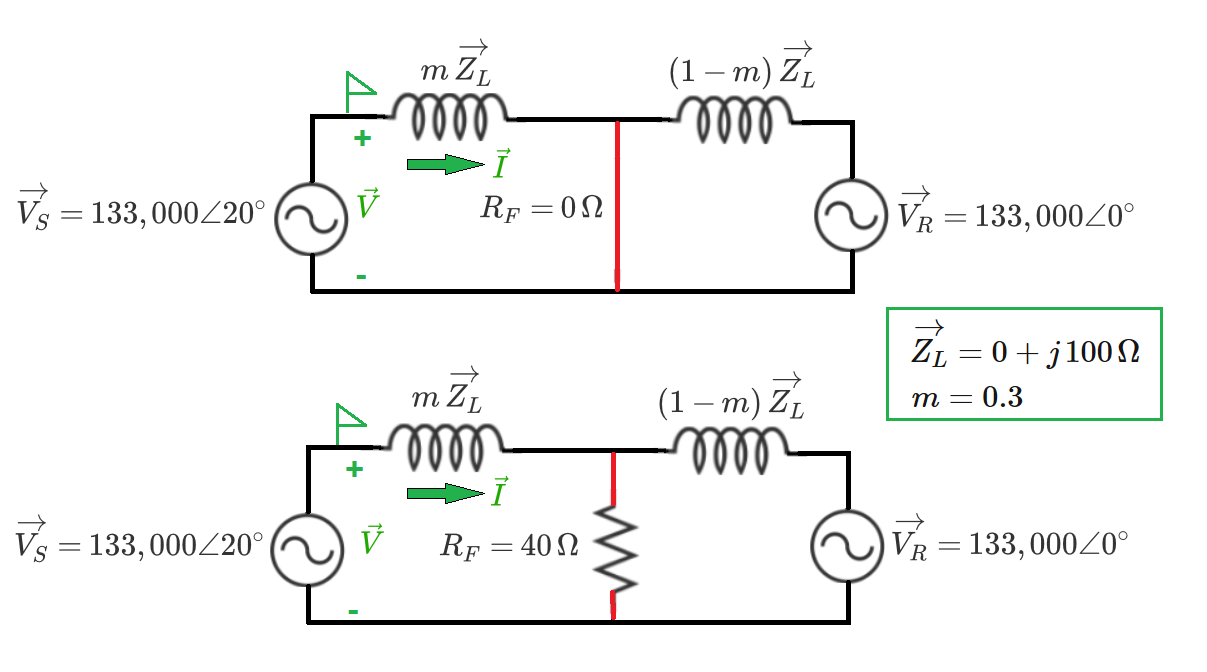
A fault locator device (shown as a green flag) is put into service at one end of a high-voltage AC transmission line. A fault (shown in red) is a short circuit from the energized transmission line to the return path (such as ground, for example).

Line and voltage source (generator) parameters are shown below. The voltage sources are assumed to have zero internal impedance, for simplicity.

When a fault occurs, the fault locator measures the current $\textcolor{#20A900}{\vec{I}}$ and voltage $\textcolor{#20A900}{\vec{V}}$ at its location. It calculates the imaginary (reactive) component of the measured impedance $(\vec{V}$ divided by $\vec{I}$ ) and divides by the total line reactance to get a "per-unit" fault location. Note that the transmission line impedance here is purely reactive $(\vec{Z_L} = 0 + j \, 100 \, \Omega)$ .

$\large{\text{Fault Location (pu) } = \frac{Im \Big [\frac{\vec{V}} {\vec{I}} \Big ]}{|\vec{Z_L}|}}$

When the fault resistance is zero (as in the first pictured case), the relay calculates the fault location perfectly, even when there is a $20^\circ$ load flow angle on the transmission line (meaning the angle difference between $\vec{V_S}$ and $\vec{V_R}$ ). For example, a fault at $30 \%$ of the line length results in a calculated per-unit fault location of $0.3$ . It also works perfectly if there is fault resistance but no load (provided that the two generator voltages have the same magnitude).

With both fault resistance and load, this simple fault locator algorithm incorrectly calculates the per-unit fault location. For this reason, more sophisticated algorithms are actually used in practice.

For a fault at $30 \% (m = 0.3)$ , with fault resistance $R_F = 40 \, \Omega$ (as in the second pictured case), and a load flow angle of $20^\circ$ , what is the calculated per-unit fault location?

Note: Real high-voltage transmission lines transmit three-phase power, but for simplicity, the line here is single-phase.