Faulted DC Circuit
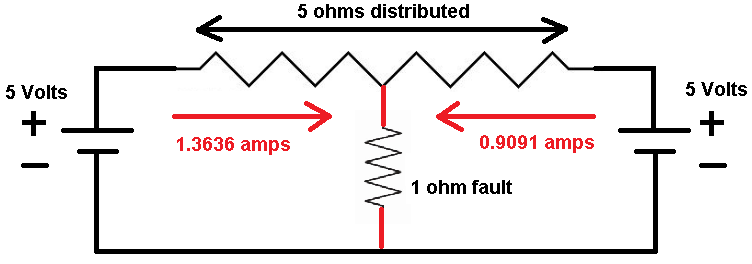
A 5-ohm distributed resistor is connected between the positive terminals of two ideal 5-volt DC batteries. The negative terminals of the batteries are connected together.
There is a 1-ohm fault (unintended connection) from some point on the distributed resistor to the negative bus. The resulting currents (both magnitude and direction) are illustrated in the above diagram.
Determine how many ohms of distributed resistance there are to the LEFT of the fault point.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
See here for circuit analysis basics. Start at the positive terminals of the batteries. Take the voltage drops through the distributed resistance portions and through the fault until the negative terminal is reached. The negative terminal is considered to be at reference potential (zero volts). The current through the fault is the sum of the currents sourced by the two batteries. Refer to the distributed resistance to the left of the fault as "R".
From the left: 5 - (1.3636 * R) - (1.3636 + 0.9091)*(1) = 0
From the right: 5 - (0.9091 * (5 - R)) - (1.3636 + 0.9091)*(1) = 0
First equation minus second equation: -1.3636 * R + (0.9091 * (5 - R)) = 0
Which becomes: R*(-1.3636 - 0.9091) = -0.9091 * 5
R is therefore equal to 2 ohms