Faulty conveyor belt
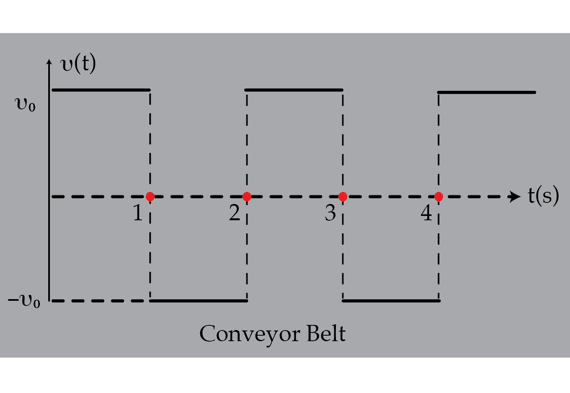
A small box is placed on a conveyor belt that moves with constant speed . Due to a technical malfunction, the belts starts moving left and right at constant speed (see the graph below). The coefficient of kinetic friction when the box moves to left, relative to the belt, is and it is when the box moves to the right, relative to the belt. As a result, of this frictional anisotropy, the box moves, on average, to the right. Assume that the conveyor belt is very long, determine the magnitude of the terminal average velocity in meters per second of the box (in the laboratory frame of reference).
Details and assumptions
Assume that .
The answer is 0.085.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we observe that the box cannot move faster than the belt, i.e., the speed of the box cannot be greater than v 0 . Second, when the box reaches either v 0 or − v 0 it stops until the belt changes its direction of motion. Using Newton's second law, we find that the acceleration to the right and left are a R = μ L g = 3 . 9 2 m / s 2 and a L = μ R g = 2 . 9 4 m / s 2 . These number suggest that the steady-state motion of the box will be described by the graph shown below. Note that the motion as described in the graph is periodic and this is why we call it steady-state (or terminal). We note that the displacement of the box when it is moving relative to the belt is always zero (in a graph of v vs. t , the displacement equals the area under the curve). Thus, the displacement of the box occurs only when it is not moving relative to the belt (see the intervals Δ t 1 and Δ t 2 ). Let Δ x 1 and Δ x 2 be the displacements during these intervals. It is not hard to find that Δ x 1 = − v 0 ( T − 2 μ R g v 0 ) < 0 and Δ x 2 = v 0 ( T − 2 μ L g v 0 ) , where T = 1 s . The total displacement during the cycle is Δ x = Δ x 2 + Δ x 1 = g 2 v 0 2 ( μ R 1 − μ L 1 ) . Finally, we find the average velocity v ˉ = 2 T Δ x = g T v 0 2 ( μ R 1 − μ L 1 ) = 0 . 0 8 5 m/s . One should note, that the above formula is not general. Note that for other values of μ R and μ L the graph shown below would be completely different. For example, if μ R = 0 then the velocity of the box would be constant and equal to v 0 .