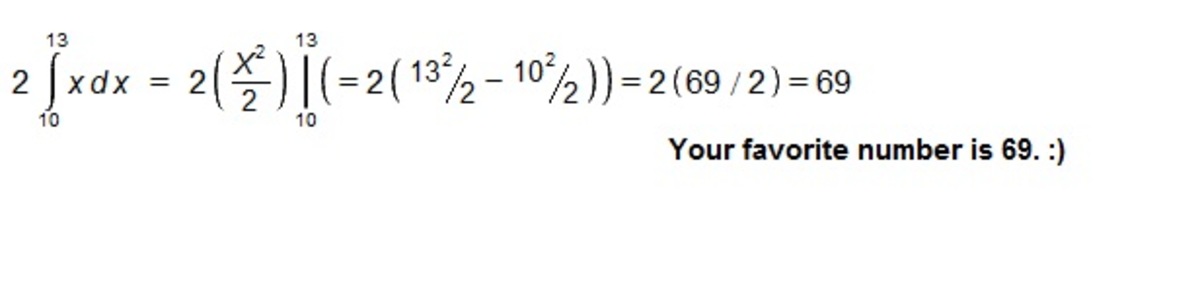Favorite Number
What is my favorite number?
Hint: ∫ 1 0 1 3 2 x d x
The answer is 69.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
∫ 1 0 1 3 2 x d x = x 2 1 0 1 3 = 1 3 2 − 1 0 2 = 1 6 9 − 1 0 0 = 6 9
Before even attempting to solve it I typed in 69 and voila!
∫ 1 0 1 3 2 x dx = x 2 ∣ 1 0 1 3 = 1 6 9 − 1 0 0 = 6 9
=x^2 =13^2-10^2 =(13+10)(13-10) =(23)(3) =69
The antiderivative of 2 x is x 2 + C my excellent stallion. Then the difference of squares is 2 3 ∗ 3 . 69 dudes!
integrate 2x get (2x^2)/2 so its X^2 (definite integral omit constant) Then 13^2 - 10^2 = 69
(You pervert...)