Favorite problem: Serbian mathematical competition 2007 - Regional level, year 2, B category
In triangle △ A B C , the reflection of its incenter over side A B is its circumcenter.
Find the measure of ∠ C in degrees.
The answer is 108.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
nice and short solution(+1), theres a typo , the angles sum up to 90 not 180, but the rest of the math is right.
excellent!
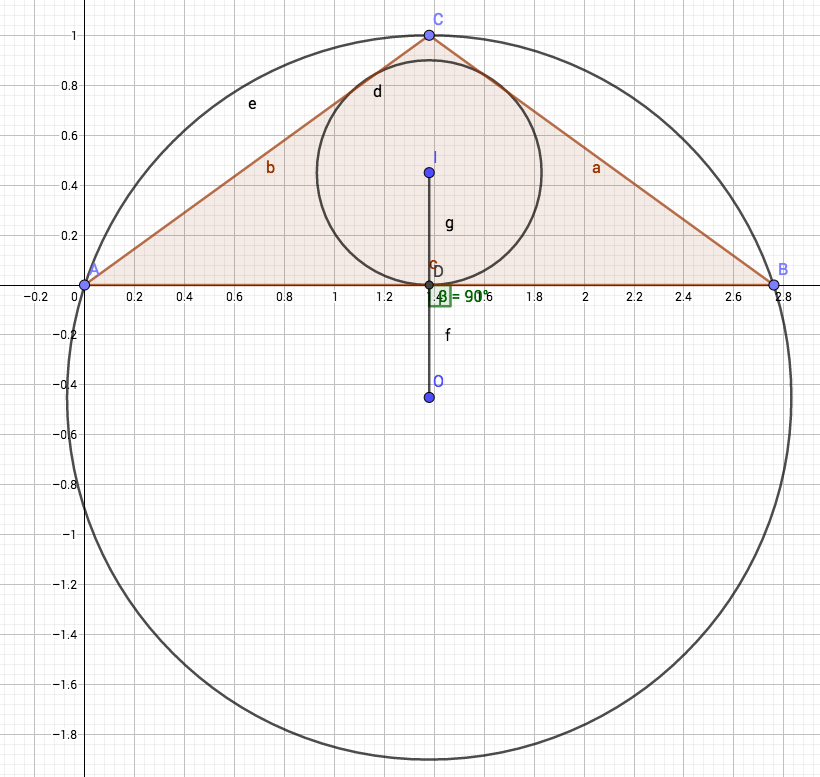 for simplicity define the triangle as the points
A
,
C
,
B
=
(
0
,
0
)
,
(
x
1
,
y
1
)
,
(
x
2
,
0
)
. by the given condition reflecting the incircle(
I
over
A
B
is just reflecting over the x axis. let the circumcenter be
O
. since the circumcenter lies on the perpendicular bisector, it's abscissa lies midway of
A
B
, and since
O
is just
I
reflected around the x axis, the abscissa of
I
lies in the middle of
A
B
. this means
Δ
A
B
C
is isosceles.
since this system now has 2 degree of freedom, we can work with two variables and later cancel them out in some division to get a formula for the angle that is constant. instead we can call the ordinate of
C
1 and make the math easier. it will be justified later as to why the solution is unique. so we have
A
,
C
,
B
=
(
0
,
0
)
,
(
x
,
1
)
,
(
2
x
,
0
)
→
A
C
,
C
B
,
A
B
=
(
x
2
+
1
,
x
2
+
1
,
2
x
)
notice that by definition of circumradius
O
C
=
R
,
O
A
=
R
, and by definition of inradius
I
D
=
r
, and due to the reflection
O
D
=
r
. then it is easy to see
C
D
+
D
O
=
C
O
→
1
+
r
=
R
. we can easily find the circumradius by using triangle
Δ
C
D
A
first
sin
(
∠
A
)
=
C
A
C
D
=
x
2
+
1
1
=
2
R
C
B
=
2
R
x
2
+
1
→
R
=
2
x
2
+
1
→
r
=
2
x
2
−
1
the semiperimeter is
2
x
2
+
1
+
x
2
+
1
+
2
x
=
x
2
+
1
+
x
. we can relate
r
and
R
by two different area formulas, i.e
r
s
=
4
R
A
B
×
B
C
×
C
A
→
2
x
2
−
1
(
x
2
+
1
+
x
)
=
4
×
2
x
2
+
1
2
x
×
x
2
+
1
×
x
2
+
1
→
(
x
2
−
1
)
(
x
2
+
1
+
x
)
=
2
x
→
x
2
−
1
=
2
x
(
x
2
+
1
−
x
)
→
3
x
2
−
1
=
2
x
x
2
+
1
→
(
3
x
2
−
1
)
2
=
4
x
2
(
x
2
+
1
)
if we define
z
=
x
2
+
1
then
(
3
z
−
7
)
2
=
4
(
z
−
1
)
z
→
5
z
2
−
3
8
z
+
4
9
=
0
→
z
=
x
2
+
1
=
5
±
2
+
2
5
notice that the smaller solution gives
R
=
2
z
≈
.
5
5
but since the circumradius is suppose to be outside the triangle for this case, it can be neglected. this leaves only one choise, and using a previous formula
sin
(
∠
A
)
=
z
1
→
∠
A
=
5
π
→
∠
C
=
π
−
2
×
5
π
=
5
3
π
=
1
0
8
de
g
and this is unique because suppose on the choice of another
C
D
=
1
a different solution was found, then that triangle should be able to be scaled down to
C
D
=
1
and the new triangle will still be a solution to the given conditions. but then it must appear as a solution to the
C
D
=
1
system, which only has one solution. hence the constraint has only one solution for the angle.
for simplicity define the triangle as the points
A
,
C
,
B
=
(
0
,
0
)
,
(
x
1
,
y
1
)
,
(
x
2
,
0
)
. by the given condition reflecting the incircle(
I
over
A
B
is just reflecting over the x axis. let the circumcenter be
O
. since the circumcenter lies on the perpendicular bisector, it's abscissa lies midway of
A
B
, and since
O
is just
I
reflected around the x axis, the abscissa of
I
lies in the middle of
A
B
. this means
Δ
A
B
C
is isosceles.
since this system now has 2 degree of freedom, we can work with two variables and later cancel them out in some division to get a formula for the angle that is constant. instead we can call the ordinate of
C
1 and make the math easier. it will be justified later as to why the solution is unique. so we have
A
,
C
,
B
=
(
0
,
0
)
,
(
x
,
1
)
,
(
2
x
,
0
)
→
A
C
,
C
B
,
A
B
=
(
x
2
+
1
,
x
2
+
1
,
2
x
)
notice that by definition of circumradius
O
C
=
R
,
O
A
=
R
, and by definition of inradius
I
D
=
r
, and due to the reflection
O
D
=
r
. then it is easy to see
C
D
+
D
O
=
C
O
→
1
+
r
=
R
. we can easily find the circumradius by using triangle
Δ
C
D
A
first
sin
(
∠
A
)
=
C
A
C
D
=
x
2
+
1
1
=
2
R
C
B
=
2
R
x
2
+
1
→
R
=
2
x
2
+
1
→
r
=
2
x
2
−
1
the semiperimeter is
2
x
2
+
1
+
x
2
+
1
+
2
x
=
x
2
+
1
+
x
. we can relate
r
and
R
by two different area formulas, i.e
r
s
=
4
R
A
B
×
B
C
×
C
A
→
2
x
2
−
1
(
x
2
+
1
+
x
)
=
4
×
2
x
2
+
1
2
x
×
x
2
+
1
×
x
2
+
1
→
(
x
2
−
1
)
(
x
2
+
1
+
x
)
=
2
x
→
x
2
−
1
=
2
x
(
x
2
+
1
−
x
)
→
3
x
2
−
1
=
2
x
x
2
+
1
→
(
3
x
2
−
1
)
2
=
4
x
2
(
x
2
+
1
)
if we define
z
=
x
2
+
1
then
(
3
z
−
7
)
2
=
4
(
z
−
1
)
z
→
5
z
2
−
3
8
z
+
4
9
=
0
→
z
=
x
2
+
1
=
5
±
2
+
2
5
notice that the smaller solution gives
R
=
2
z
≈
.
5
5
but since the circumradius is suppose to be outside the triangle for this case, it can be neglected. this leaves only one choise, and using a previous formula
sin
(
∠
A
)
=
z
1
→
∠
A
=
5
π
→
∠
C
=
π
−
2
×
5
π
=
5
3
π
=
1
0
8
de
g
and this is unique because suppose on the choice of another
C
D
=
1
a different solution was found, then that triangle should be able to be scaled down to
C
D
=
1
and the new triangle will still be a solution to the given conditions. but then it must appear as a solution to the
C
D
=
1
system, which only has one solution. hence the constraint has only one solution for the angle.
I think that your solution is very complex and involves a lot of calculation, as this problem can be solved by elementry methods of 7th Standard.
Log in to reply
well all the math done here can be done using knowledge of freshmen and sophomore level math(algebra i and geometry), however did take some time, what would be the easier way.
Log in to reply
I will surely post my solution, and by the way, I commented that because I haven't yet learnt Trignometry.
@Aareyan Manzoor , My solution was same as Steve Yuan's.
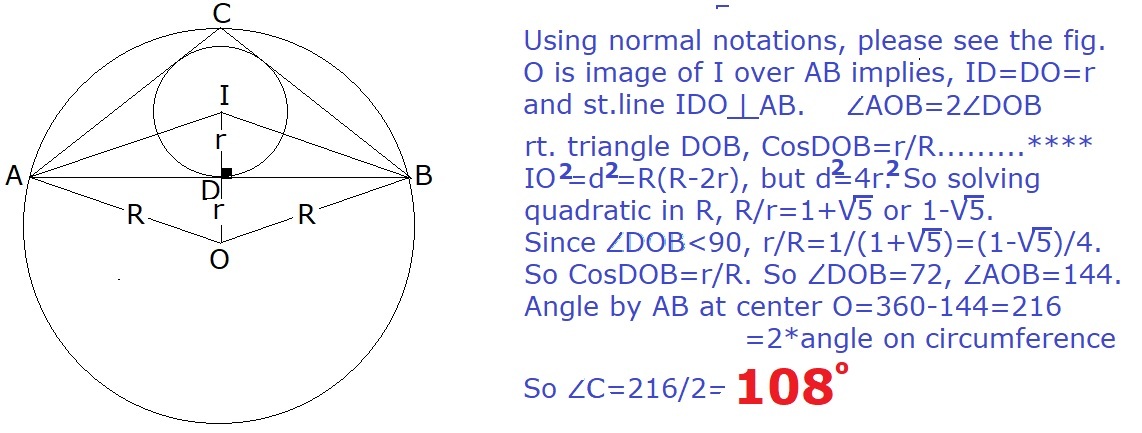
Let O , I be the circumcenter and incenter of △ A B C , respectively. By the reflection condition, it is clear that △ A B C is isosceles, as A I is an angle bisector, median, and altitude. Let ∠ C A B = ∠ C B A = θ . We have
∠ A I O = ∠ A O I (reflection) = 2 ∠ C B A (inscribed angle) = 2 θ ,
and ∠ I A B = 2 θ . Since these two angles are the angles of a right triangle, we have 2 θ + 2 θ = 9 0 ∘ , or θ = 3 6 ∘ . Therefore, ∠ C = 1 8 0 ∘ − 2 θ = 1 8 0 ∘ − 2 ( 3 6 ∘ ) = 1 0 8 ∘ .