Feed the goat, help the farmer
You are a farmer, with a round fenced field of radius 1 0 meters. You tie your goat to the fence with a rope, and realize that the goat can eat exactly 2 1 of the field. How long is the rope?
Note: You can use a computational solver for the last step of the problem.
The answer is 11.58.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Really nice solution @Pratik Shastri I had a lot problem with this one huh.
How do we solve the final equation?
Can anyone believe that I get through the last step purely using manual calculator?
That's not angle BOP that suppose to be angle OBP
Area of the sector =alpha×r^2 is enough to say
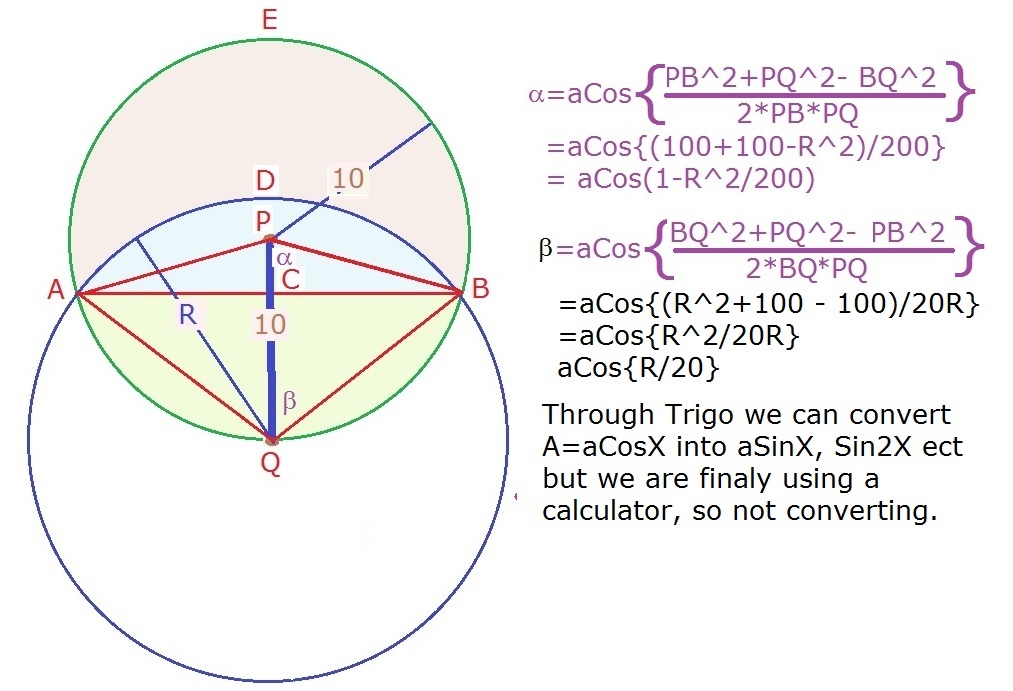
Let C 1 be the circle with radius 1 0 .
C 2 be the circle with unknown radius r .
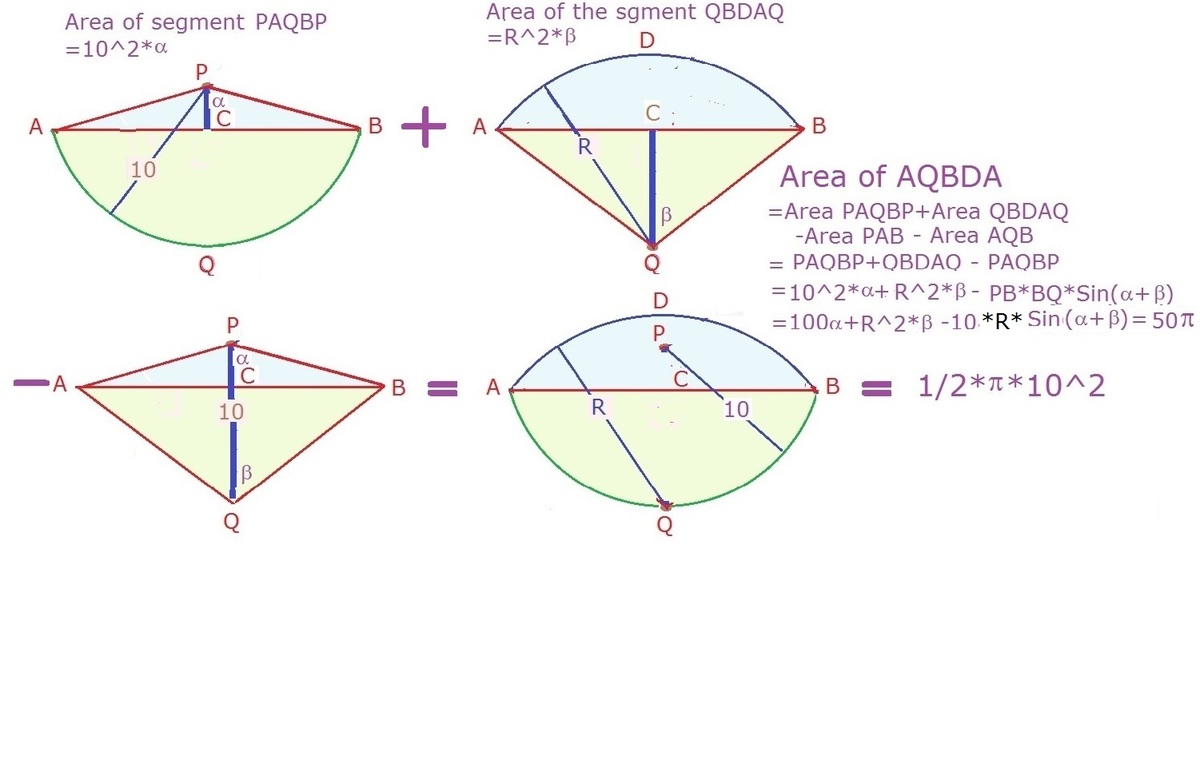
The area that exactly 2 1 of the field is 2 1 1 0 2 π = 5 0 π
The two segments bounded by the two circles C 1 & C 2 is equal to 5 0 π
Let A & B be the angle subtended by the arc formed by C 1 & C 2 .
Segment at C 1 is equal to 1 0 2 π ( 3 6 0 A ) − 2 1 0 2 sin A
Segment at C 2 is equal to r 2 π ( 3 6 0 B ) − 2 r 2 sin B
[ 1 0 2 π ( 3 6 0 A ) − 2 1 0 2 sin A ] + [ r 2 π ( 3 6 0 B ) − 2 r 2 sin B ] = 5 0 π ---> e q . 1
sin 4 A = ( 2 ) ( 1 0 ) r
r = 2 0 sin 4 A ---> e q . 2
2 B = 9 0 − 4 A
B = 2 3 6 0 − A ---> e q . 3
Substituting e q . 2 & e q . 3 in e q . 1 will result to:
1 8 5 ( A π − 1 8 0 sin A ) + 7 2 0 ( 2 0 sin 4 A ) 2 [ ( 3 6 0 − A ) π − 3 6 0 sin 2 A ] = 5 0 π
Note: All values of angles in the above formula are in degree unit.
Solve for angle A
A = 1 4 1 . 6 2 3 3 5 5 3 d e g
solve for radius r by substituting A = 1 4 1 . 6 2 3 3 5 5 3 d e g to e q . 2
r = 1 1 . 5 8 7 2 8 4 7 3 m
How are you so damn good at geometry? Could you suggest me some way to improve?
Amazing solution Partick sastri.
T
h
e
g
o
a
t
i
s
t
i
e
d
a
t
Q
.
F
r
o
m
t
h
e
a
b
o
v
e
w
e
s
e
e
"
f
(
R
)
=
1
0
0
∗
C
o
s
−
1
(
1
−
1
0
0
R
2
+
2
R
2
∗
C
o
s
−
1
(
2
0
R
−
1
0
R
∗
S
i
n
(
C
o
s
−
1
(
1
−
1
0
0
R
2
)
+
C
o
s
−
1
(
1
−
2
0
R
)
)
−
5
0
∗
π
"
S
i
n
c
e
R
h
a
s
t
o
b
e
g
r
e
a
t
e
r
t
h
a
n
1
0
,
t
h
e
v
a
l
u
e
s
t
r
i
e
d
w
e
r
e
R
=
1
1
,
R
=
1
2
,
R
=
1
1
.
5
,
R
=
1
1
.
6
,
a
n
d
t
h
e
n
r
e
f
i
n
e
d
i
t
t
o
R
=
1
1
.
5
8
7
2
8
5
.
.
S
o
s
t
o
p
p
e
d
a
t
f
(
1
1
.
5
8
7
2
8
5
)
=
5
.
9
5
8
1
E
−
6
.
I
n
s
t
e
a
d
o
f
0
t
h
i
s
i
s
t
h
e
e
r
r
o
r
.
B
y
t
h
e
w
a
y
t
h
e
a
n
s
w
e
r
s
h
o
u
l
d
h
a
v
e
b
e
e
n
1
1
.
5
9
.
Lets say that the circle with center A (and radius 1 0 m ) is the field and the goat is tied at point B .
So, the goat can move around in an area equivalent to the area of the circle with center B . Lets also assume that the length of the rope is r . Hence, the radius of this circle also is r .
What we'll do is break the required area into two parts (segments) A 1 and A 2 , find their area, and add them up and finally equate the resulting expression with 2 π 1 0 2 which is 5 0 π
A 1 + A 2 = A which is the required area.
→ Consider the following--
∙ P Q = 2 s
∙ O B = p , so O A = ( 1 0 − p ) as A B = 1 0 (Radius of the field)
Now, applying the Pythagoras theorem on △ B O P and △ A O P respectively, we get
→ r 2 = s 2 + p 2 and
→ 1 0 0 = ( 1 0 − p ) 2 + s 2 .
Solving for s and p , we find that
→ s = 2 0 r 4 0 0 − r 2
and
→ p = 2 0 r 2
Now, lets consider △ B P Q and the arc subtended by it.
Area of the segment( A 1 )=(Area of the sector)-(area of the triangle).
Lets call ∠ O B P as α .
So, cos α = r p = r 2 0 r 2 = 2 0 r .
→ α = cos − 1 ( 2 0 r )
Hence the area of the sector = 2 π 2 α π r 2
= r 2 cos − 1 ( 2 0 r )
Now, area of △ P Q B = 2 1 × base × height
= 2 1 × 2 s × p
= 4 0 0 r 3 4 0 0 − r 2
Subtracting the area of the triangle from that of the sector yields the area of the segment A 1 = r 2 cos − 1 ( 2 0 r ) − 4 0 0 r 3 4 0 0 − r 2
or simply
A 1 = r 2 cos − 1 ( 2 0 r ) − s p
Similarly, calculating the area of the other segment A 2 yields
A 2 = 1 0 0 cos − 1 ( 2 0 0 2 0 0 − r 2 ) − 2 r 4 0 0 − r 2 + s p
So, A 1 + A 2 = A = 1 0 0 cos − 1 ( 2 0 0 2 0 0 − r 2 ) − 2 r 4 0 0 − r 2 + r 2 cos − 1 ( 2 0 r )
Now we equate A with half the area of the field, which comes out to be 5 0 π
So, the final equation stands as follows
1 0 0 cos − 1 ( 2 0 0 2 0 0 − r 2 ) − 2 r 4 0 0 − r 2 + r 2 cos − 1 ( 2 0 r ) = 5 0 π
Solving for r gives r = 1 1 . 5 8 m