Feel the Gravity

Classical Mechanics Level 5

Two balls of mud are hurtling above the Earth, as shown below.

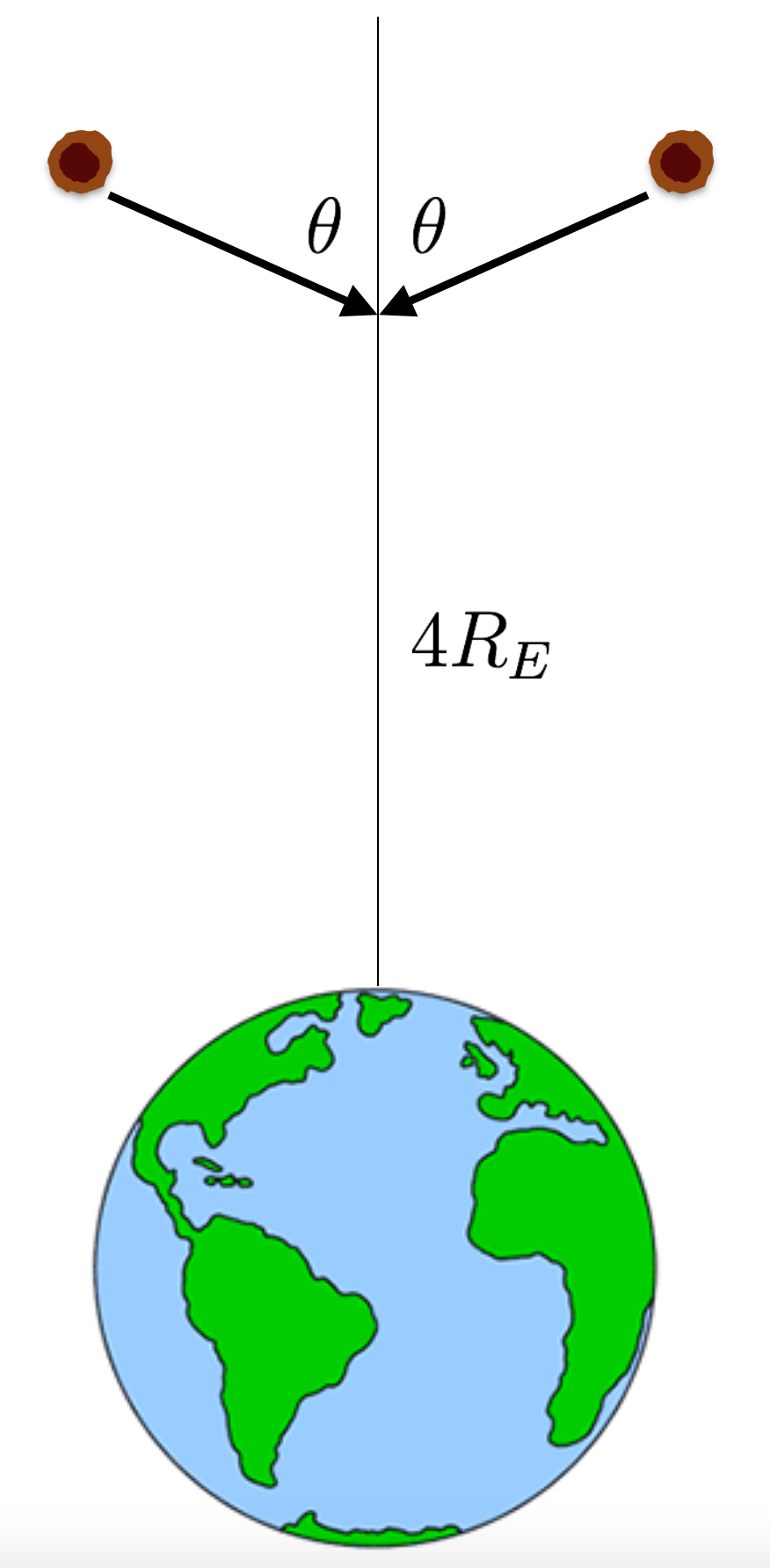
The balls collide at a height of 4 R E 4R_E from the surface of the Earth, stick together, and start to fall straight down toward the Earth. Find the time (in seconds) it takes for the composite mudball to reach the surface of the Earth.

Details and Assumptions:

  • The mud balls move with speed 512 m / s \SI{512}{\meter/\second} just before collision.
  • The radius of the Earth is R E = 6 400 km . R_E = \SI{6400}{\kilo\meter}.
  • θ = 6 0 ∘ . \theta = 60^\circ.
  • The mass of the Earth is M E = 6 × 1 0 24 kg . M_E = \SI{6e24}{\kilo\gram}.
  • G = 6.67 × 1 0 − 11 N m 2 / k g 2 . G = \SI[per-mode=symbol]{6.67e-11}{\newton\meter\squared\per\kilo\gram\squared}.
  • Ignore the effect of wind resistance. -This problem is Original ! :)


The answer is 9025.72.

View wiki
A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

According to law of conservation of momentum,

m × 256 + m × 256 = 2 m v m \times 256 + m \times 256 = 2 m v

v = 256 v = 256

Now using law of conservation of energy at height x x is

− 2 G M m 5 R + 1 2 × 2 m × ( 256 ) 2 = − 2 G M m x + 1 2 2 m v 2 \frac{-2GMm}{5R} + \frac{1}{2} \times 2m \times (256)^2 = \frac{-2GMm}{x} + \frac{1}{2} 2 m v^2

Now v = d x d t v = \frac{dx}{dt}

− 2 G M 5 R + 1 2 × 2 × ( 256 ) 2 + − 2 G M x = 1 2 2 ( d x d t ) 2 \frac{-2GM}{5R} + \frac{1}{2} \times 2 \times (256)^2 +\frac{-2GM}{x} = \frac{1}{2} 2 (\frac{dx}{dt})^2

− 2 G M 5 R + 1 2 × 2 × ( 256 ) 2 + − 2 G M x = d x d t \sqrt{\frac{-2GM}{5R} + \frac{1}{2} \times 2 \times (256)^2 +\frac{-2GM}{x}} = \frac{dx}{dt}

3 Helpful 0 Interesting 0 Brilliant 0 Confused

but how do you solve the differential equation?

alan li - 4 years, 6 months ago

Log in to reply

in case of 1/root(1+(1/x)) you take x as tan^2 t, then continuing you get (2 sin^2 t / cos^3 t) for which you split sin^2 as 1 - cos^2 after which it gets simple. Here adjust the constants and use the above idea.

Ashwath Bhat - 4 years, 5 months ago

If you would like to integrate the differential expression successfully by hand, you would need to use integration by substitution that I tried, followed by integration by parts. The calculus employed here is pretty tedious but I think its well-worth it though painful.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...