Fence Builder Logic

Logic Level 2

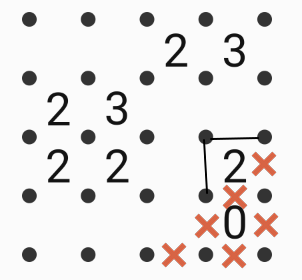
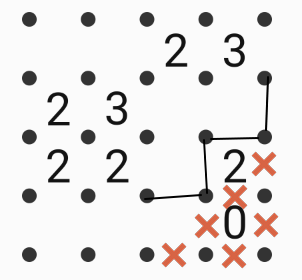
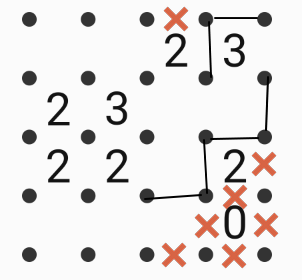
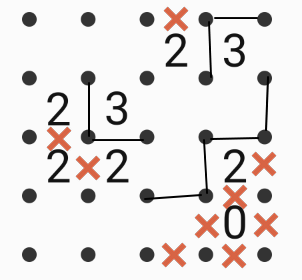
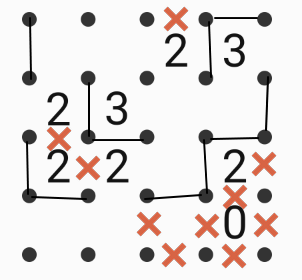
Connect adjacent dots using only vertical and horizontal line segments to make a "fence" that encloses a single region. The numbers indicate exactly how many line segments surround it; locations without numbers may be surrounded by any number of line segments. The diagram above is an example of a completed puzzle.

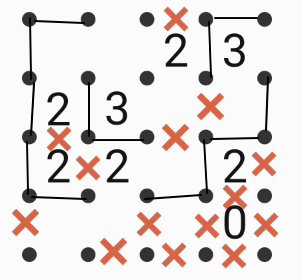
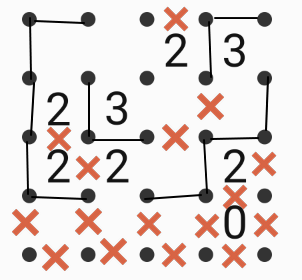
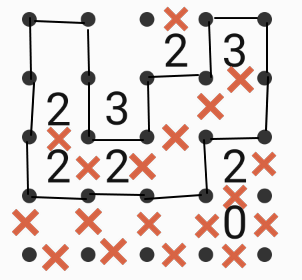
Fence in this diagram with the same rules. There is only one solution. How many numbers will be inside the fenced area?

3 4 5 6 7

2 solutions

Pi Han Goh
Nov 12, 2016

Step 01 :

Step 02 :

Step 03 :

Step 04 :

Step 05 :

Step 06 :

Step 07 :

Step 08 :

Step 09 :

Step 10 :

Could you please explain the steps? step01 is trivial. From step 02, how x's are marked?

Krishna Chaitanya Marreddy - 4 years, 7 months ago

Suppose you draw the lines where the new "x"s are marked in step 2, then where should these lines "move" afterwards? It's impossible right? That's why it's an "x".

What else are you confused on?

Pi Han Goh - 4 years, 7 months ago

I agree that having a short phrase/sentence to explain how each step was achieved would be helpful. It might not be to each step, but giving an initial overview of the main ideas / approaches used would be helpful. E.g.

The degree of each vertex is exactly 2 or 0.
We use x to mark out places where we know the fences cannot be built
No fence around a square of 0
Fences cannot connect to a vertex whose allowable degree is less than 2.

Calvin Lin Staff - 4 years, 6 months ago

Vishwash Kumar S
Nov 11, 2016

Fence Builder Logic

2 solutions

0 pending reports