Fenced Semicircle 2
Geometry
Level
3
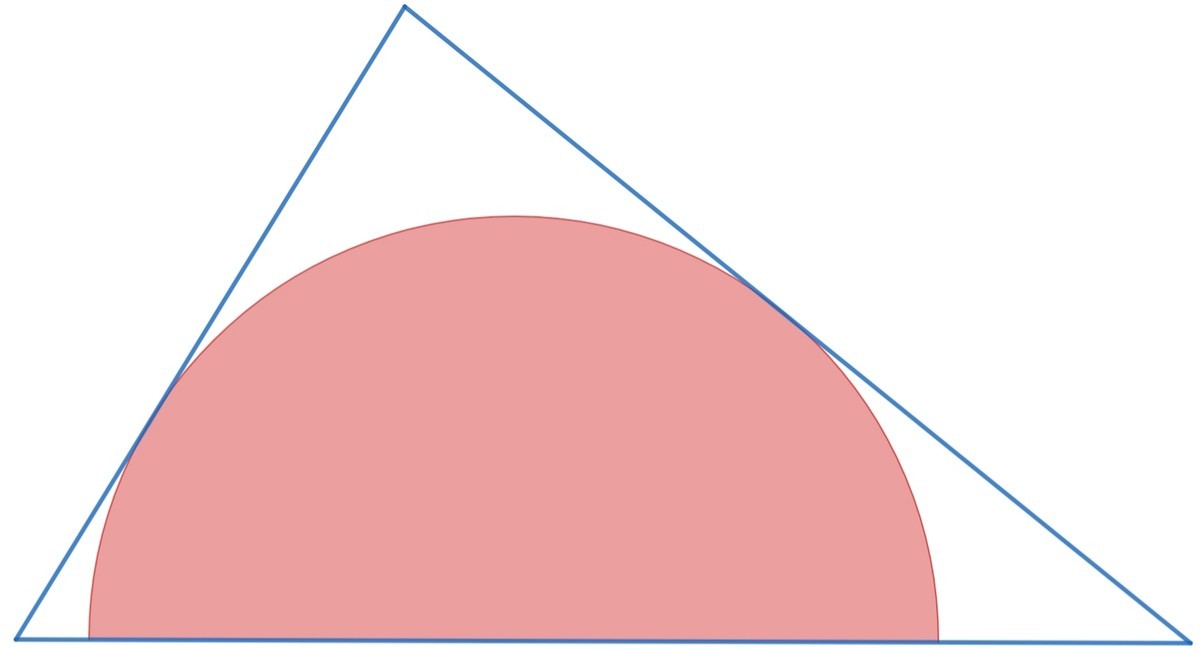
A variable triangle circumscribes a semicircle of unit radius, as shown.
Find the minimum area of the triangle.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the angles subtended by the radii to the two slant sides of the triangle are x and y as marked, then the triangle has base length sec x + sec y . A little coordinate geometry (solving the equations of the two slant lines simultaneously) gives us that the triangle has height sin ( x + y ) cos x + cos y .
Thus the triangle has area A = 2 sin ( x + y ) ( sec x + sec y ) ( cos x + cos y ) = 2 cos x cos y sin ( x + y ) ( cos x + cos y ) 2 = 2 sin ( x + y ) 1 ( cos y cos x + cos x cos y ) 2 ≥ sin ( x + y ) 2 ≥ 2 with the minimum value of 2 achieved when x = y = 4 5 ∘ .