Fermat's Distance

The best-known property of the 1st Fermat point is that it minimizes the sum of the distances to a triangle's vertices. In △ A B C , if F is the Fermat point, find A F + B F + C F , express it as a + b , where a and b are positive integers, and submit a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
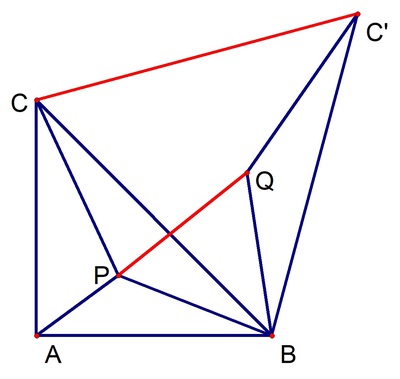 Rotate triangle
B
P
C
through
6
0
∘
about
B
to form triangle
B
Q
C
′
, so that
B
P
Q
and
B
C
C
′
are equilateral triangles. Then
P
Q
=
P
B
and
Q
C
′
=
P
C
, so that
P
A
+
P
B
+
P
C
=
A
P
+
P
Q
+
Q
C
′
≥
A
C
′
, and hence we deduce that
A
P
+
B
P
+
C
P
≥
A
C
′
, and this minimum distance is achieved when
P
is the first Fermat point of
A
B
C
, which is the point where
P
sutends angle
1
2
0
∘
at each of the arcs
A
B
,
B
C
and
A
C
. In this case
A
C
′
=
2
1
+
2
×
2
3
=
2
3
+
1
=
2
+
3
making the answer
2
+
3
=
5
.
Rotate triangle
B
P
C
through
6
0
∘
about
B
to form triangle
B
Q
C
′
, so that
B
P
Q
and
B
C
C
′
are equilateral triangles. Then
P
Q
=
P
B
and
Q
C
′
=
P
C
, so that
P
A
+
P
B
+
P
C
=
A
P
+
P
Q
+
Q
C
′
≥
A
C
′
, and hence we deduce that
A
P
+
B
P
+
C
P
≥
A
C
′
, and this minimum distance is achieved when
P
is the first Fermat point of
A
B
C
, which is the point where
P
sutends angle
1
2
0
∘
at each of the arcs
A
B
,
B
C
and
A
C
. In this case
A
C
′
=
2
1
+
2
×
2
3
=
2
3
+
1
=
2
+
3
making the answer
2
+
3
=
5
.
Well done, as usual.