Feuerbach's Bow-Tie
 The points
A
,
B
lie on the diameter of a unit circle, and
C
is a third point on that circle, forming a triangle
A
B
C
. The Feuerbach point
F
e
of a (non-equilateral) triangle is the point where that triangle's incircle and nine-point circle are tangential to each other. The locus of the Feuerbach point of the triangle
A
B
C
, as
C
varies, forms an intriguing bow-tie shaped outline. It can be shown that the area enclosed by this bow-tie is of the form
a
−
c
b
π
where
a
,
b
,
c
are positive integers and
b
,
c
are coprime. Find the value of
a
+
b
+
c
.
The points
A
,
B
lie on the diameter of a unit circle, and
C
is a third point on that circle, forming a triangle
A
B
C
. The Feuerbach point
F
e
of a (non-equilateral) triangle is the point where that triangle's incircle and nine-point circle are tangential to each other. The locus of the Feuerbach point of the triangle
A
B
C
, as
C
varies, forms an intriguing bow-tie shaped outline. It can be shown that the area enclosed by this bow-tie is of the form
a
−
c
b
π
where
a
,
b
,
c
are positive integers and
b
,
c
are coprime. Find the value of
a
+
b
+
c
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
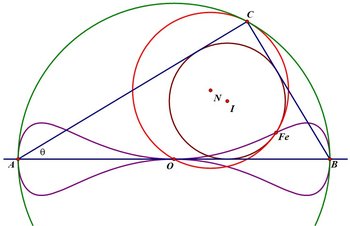 If we let
∠
B
A
C
=
θ
for
0
<
θ
<
2
1
π
(so that
C
is in the upper semicircle), then the vertices of the triangle
A
B
C
are
A
(
−
1
,
0
)
B
(
1
,
0
)
C
(
cos
2
θ
,
sin
2
θ
)
As has been shown in previous problems of this type, the incentre
I
of
A
B
C
has coordinates
I
(
cos
θ
−
sin
θ
,
cos
θ
+
sin
θ
−
1
)
(note that
cos
θ
+
sin
θ
−
1
is the inradius). Since
A
B
C
is right-angled, the orthocentre of
A
B
C
is the vertex
C
, and so the nine-point centre
N
is the midpoint of
O
C
, and hence has coordinates
N
(
2
1
cos
2
θ
,
2
1
sin
2
θ
)
We calculate that
I
N
=
2
1
(
3
−
2
cos
θ
−
2
sin
θ
)
, and so (since the radius of the nine-point circle is half that of the outcircle, namely
2
1
)
O
F
e
=
O
N
+
3
−
2
cos
θ
−
2
sin
θ
1
N
I
It is useful at this stage to introduce the coordinate
u
=
θ
−
4
1
π
, so that
F
e
has coordinates
(
X
(
u
)
,
Y
(
u
)
)
, where
X
(
u
)
=
3
−
2
2
cos
u
2
sin
u
(
2
cos
2
u
−
2
cos
u
−
1
)
Y
(
u
)
=
3
−
2
2
cos
u
2
sin
2
u
(
2
cos
u
−
1
)
We find that
X
′
(
u
)
Y
(
u
)
=
Z
(
cos
u
)
, where
Z
(
c
)
=
(
3
−
2
2
c
)
3
2
(
1
−
c
2
)
(
2
c
−
1
)
(
1
0
−
1
5
2
c
−
4
c
2
+
2
2
2
c
3
−
1
6
c
4
)
=
−
1
6
1
5
+
4
1
2
c
+
8
1
7
c
2
−
4
3
2
c
3
−
2
c
4
+
6
4
(
3
−
2
2
c
)
3
1
−
3
2
(
3
−
2
2
c
)
2
5
+
6
4
(
3
−
2
2
c
)
4
1
Thus the desired area is
Δ
, where
−
2
1
Δ
=
∫
−
4
1
π
4
1
π
Z
(
cos
u
)
d
u
=
∫
−
4
1
π
4
1
π
(
−
1
6
1
5
+
4
1
2
cos
u
+
8
1
7
cos
2
u
−
4
3
2
cos
3
u
−
2
cos
4
u
)
d
u
+
6
4
4
1
Q
1
−
3
2
5
Q
2
+
6
4
1
Q
3
=
−
1
6
1
1
−
1
6
5
π
+
6
4
4
1
Q
1
−
3
2
5
Q
2
+
6
4
1
Q
3
where
Q
j
=
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
d
u
j
∈
N
∪
{
0
}
Now, integrating by parts,
Q
j
=
3
Q
j
+
1
−
2
2
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
1
cos
u
d
u
=
3
Q
j
+
1
−
2
2
{
[
(
3
−
2
2
cos
u
)
j
+
1
sin
u
]
−
4
1
π
4
1
π
+
2
2
(
j
+
1
)
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
2
sin
2
u
d
u
}
=
3
Q
j
+
1
−
4
−
8
(
j
+
1
)
Q
j
+
2
+
8
(
j
+
1
)
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
2
cos
2
u
d
u
=
3
Q
j
+
1
−
4
−
8
(
j
+
1
)
Q
j
+
2
+
(
j
+
1
)
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
2
9
−
6
(
3
−
2
2
cos
u
)
+
(
3
−
2
2
cos
u
)
2
d
u
=
3
Q
j
+
1
−
4
−
8
(
j
+
1
)
Q
j
+
2
+
(
j
+
1
)
(
9
Q
j
+
2
−
6
Q
j
+
1
+
Q
j
)
so we obtain the recurrence relation
j
Q
j
−
3
(
2
j
+
1
)
Q
j
+
1
+
(
j
+
1
)
Q
j
+
2
=
4
j
≥
0
Now
Q
0
=
2
1
π
and
Q
1
=
2
∫
0
4
1
π
3
−
2
2
cos
u
d
u
=
4
∫
0
2
−
1
(
3
−
2
2
)
+
(
3
+
2
2
)
t
2
d
t
=
4
(
3
−
2
2
)
∫
0
2
−
1
(
3
−
2
2
)
2
+
t
2
d
t
=
4
tan
−
1
(
2
+
1
)
=
2
3
π
using the substitution
t
=
tan
2
1
θ
. Thus we deduce that
Q
2
=
4
+
2
9
π
and
Q
3
=
2
0
+
2
3
9
π
, and hence
Δ
=
8
1
1
+
8
5
π
−
3
2
4
1
Q
1
+
1
6
5
Q
2
−
3
2
1
Q
3
=
2
−
2
1
π
making the answer
2
+
1
+
2
=
5
.
If we let
∠
B
A
C
=
θ
for
0
<
θ
<
2
1
π
(so that
C
is in the upper semicircle), then the vertices of the triangle
A
B
C
are
A
(
−
1
,
0
)
B
(
1
,
0
)
C
(
cos
2
θ
,
sin
2
θ
)
As has been shown in previous problems of this type, the incentre
I
of
A
B
C
has coordinates
I
(
cos
θ
−
sin
θ
,
cos
θ
+
sin
θ
−
1
)
(note that
cos
θ
+
sin
θ
−
1
is the inradius). Since
A
B
C
is right-angled, the orthocentre of
A
B
C
is the vertex
C
, and so the nine-point centre
N
is the midpoint of
O
C
, and hence has coordinates
N
(
2
1
cos
2
θ
,
2
1
sin
2
θ
)
We calculate that
I
N
=
2
1
(
3
−
2
cos
θ
−
2
sin
θ
)
, and so (since the radius of the nine-point circle is half that of the outcircle, namely
2
1
)
O
F
e
=
O
N
+
3
−
2
cos
θ
−
2
sin
θ
1
N
I
It is useful at this stage to introduce the coordinate
u
=
θ
−
4
1
π
, so that
F
e
has coordinates
(
X
(
u
)
,
Y
(
u
)
)
, where
X
(
u
)
=
3
−
2
2
cos
u
2
sin
u
(
2
cos
2
u
−
2
cos
u
−
1
)
Y
(
u
)
=
3
−
2
2
cos
u
2
sin
2
u
(
2
cos
u
−
1
)
We find that
X
′
(
u
)
Y
(
u
)
=
Z
(
cos
u
)
, where
Z
(
c
)
=
(
3
−
2
2
c
)
3
2
(
1
−
c
2
)
(
2
c
−
1
)
(
1
0
−
1
5
2
c
−
4
c
2
+
2
2
2
c
3
−
1
6
c
4
)
=
−
1
6
1
5
+
4
1
2
c
+
8
1
7
c
2
−
4
3
2
c
3
−
2
c
4
+
6
4
(
3
−
2
2
c
)
3
1
−
3
2
(
3
−
2
2
c
)
2
5
+
6
4
(
3
−
2
2
c
)
4
1
Thus the desired area is
Δ
, where
−
2
1
Δ
=
∫
−
4
1
π
4
1
π
Z
(
cos
u
)
d
u
=
∫
−
4
1
π
4
1
π
(
−
1
6
1
5
+
4
1
2
cos
u
+
8
1
7
cos
2
u
−
4
3
2
cos
3
u
−
2
cos
4
u
)
d
u
+
6
4
4
1
Q
1
−
3
2
5
Q
2
+
6
4
1
Q
3
=
−
1
6
1
1
−
1
6
5
π
+
6
4
4
1
Q
1
−
3
2
5
Q
2
+
6
4
1
Q
3
where
Q
j
=
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
d
u
j
∈
N
∪
{
0
}
Now, integrating by parts,
Q
j
=
3
Q
j
+
1
−
2
2
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
1
cos
u
d
u
=
3
Q
j
+
1
−
2
2
{
[
(
3
−
2
2
cos
u
)
j
+
1
sin
u
]
−
4
1
π
4
1
π
+
2
2
(
j
+
1
)
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
2
sin
2
u
d
u
}
=
3
Q
j
+
1
−
4
−
8
(
j
+
1
)
Q
j
+
2
+
8
(
j
+
1
)
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
2
cos
2
u
d
u
=
3
Q
j
+
1
−
4
−
8
(
j
+
1
)
Q
j
+
2
+
(
j
+
1
)
∫
−
4
1
π
4
1
π
(
3
−
2
2
cos
u
)
j
+
2
9
−
6
(
3
−
2
2
cos
u
)
+
(
3
−
2
2
cos
u
)
2
d
u
=
3
Q
j
+
1
−
4
−
8
(
j
+
1
)
Q
j
+
2
+
(
j
+
1
)
(
9
Q
j
+
2
−
6
Q
j
+
1
+
Q
j
)
so we obtain the recurrence relation
j
Q
j
−
3
(
2
j
+
1
)
Q
j
+
1
+
(
j
+
1
)
Q
j
+
2
=
4
j
≥
0
Now
Q
0
=
2
1
π
and
Q
1
=
2
∫
0
4
1
π
3
−
2
2
cos
u
d
u
=
4
∫
0
2
−
1
(
3
−
2
2
)
+
(
3
+
2
2
)
t
2
d
t
=
4
(
3
−
2
2
)
∫
0
2
−
1
(
3
−
2
2
)
2
+
t
2
d
t
=
4
tan
−
1
(
2
+
1
)
=
2
3
π
using the substitution
t
=
tan
2
1
θ
. Thus we deduce that
Q
2
=
4
+
2
9
π
and
Q
3
=
2
0
+
2
3
9
π
, and hence
Δ
=
8
1
1
+
8
5
π
−
3
2
4
1
Q
1
+
1
6
5
Q
2
−
3
2
1
Q
3
=
2
−
2
1
π
making the answer
2
+
1
+
2
=
5
.
@Mark Hennings I have to admit, this is a very nice figure.