Feuerbach's Foil
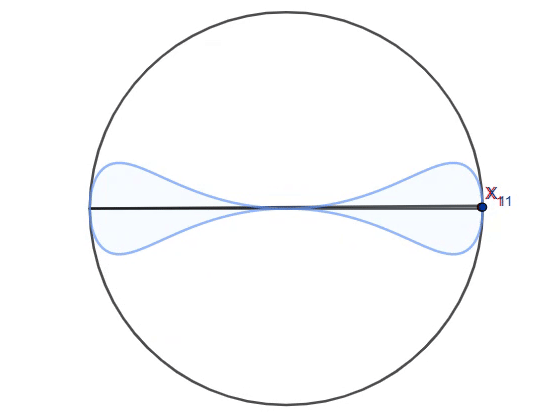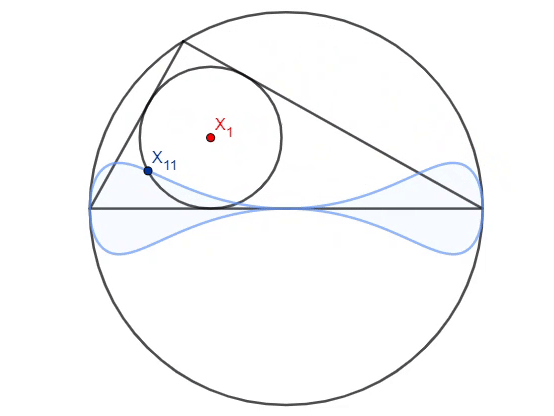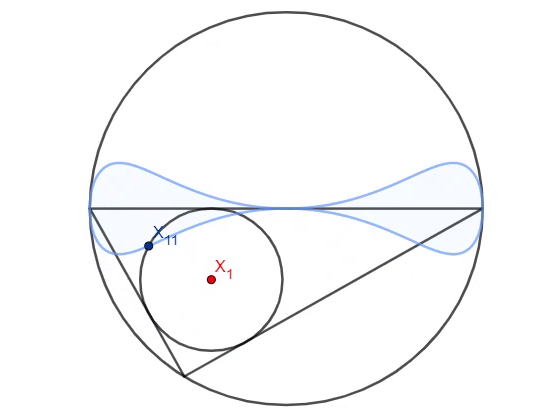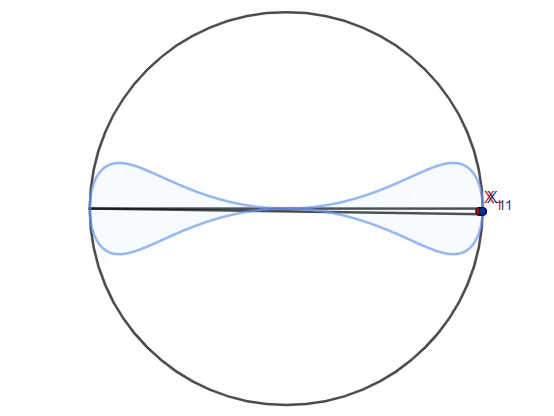
In a unit circle, two fixed endpoints of the diameter and a point selected on the circumference forms a triangle. The point on the circumference is rotated counterclockwise, so that the locus of the Feuerbach point forms a double-bulb-shaped curve (marked in blue on the animation). It can be shown that the area enclosed by the locus is equal to
where are positive integers and . Find the value of .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Bizarrely, this problem and mine seem to have been posted almost simultaneously!