Feynman Checkerboard!
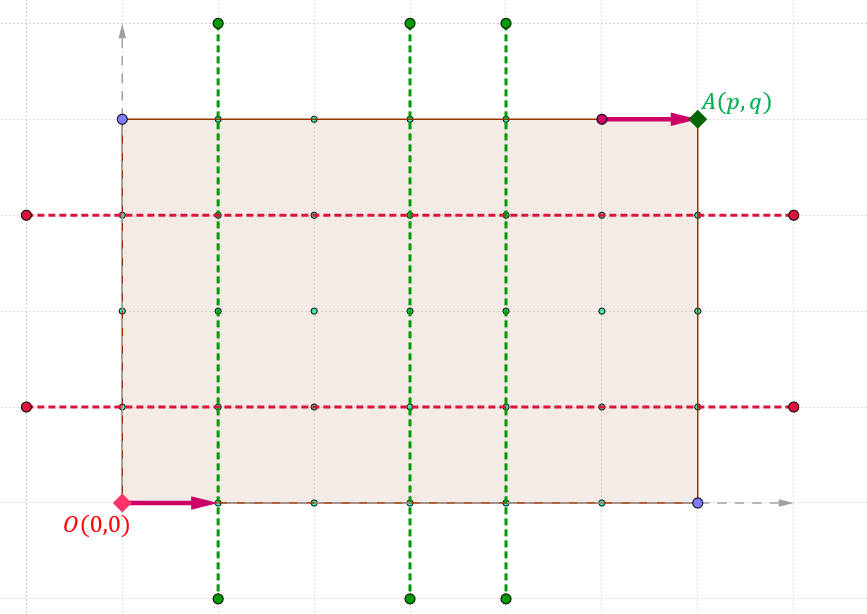
Richard P Feynman starts his journey from O = ( 0 , 0 ) towards A = ( 1 0 , 6 ) . He can only go in the + x and + y directions along the lattice, and he must turn exactly 7 times. An example path is shown above, with the yellow dots indicating turns.
How many ways can Feynman travel from O to A in this way?
Bonus : Consider the general case, traveling from ( 0 , 0 ) to ( p , q ) with exactly r turns.
The answer is 1680.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Interesting that you got the solution from 9!5!/(4!5!3!2!) + 9!5!/(6!3!4!1!). I thought that with even numbers of "up" and "right" movements it was easier to express as
2 x 9!5!/(6!3!3!2!).
Doesn't this double count identical paths? There's 24 ways to arrange the distances {1,2,3,4} but only 4 distinct ways to arrange {1,1,1,7}, and for that reason I am curious whether it's possible the above method doesn't over count. I got 1060 ways (10 70+10 36).
your general formula is wrong. for example for (3,3) grid and 3 turns, there are 8 paths. your formula suggests only 4.
The error in your analysis is that the last turn has no option and must occur on the last row/column (while the other coordinate was decide by the previous turn), so there are actually only r − 1 turns to consider.
{ If r is even: If r is odd: ( r / 2 p − 1 ) ( r / 2 − 1 q − 1 ) + ( r / 2 − 1 p − 1 ) ( r / 2 q − 1 ) 2 ( ( r − 1 ) / 2 p − 1 ) ( ( r − 1 ) / 2 q − 1 )
Alternatively to stars and bars; you can also consider: if we go up first, then the other ( r − 1 ) / 2 upward movements must occur in distinct columns that cannot be the first or last. There are p + 1 columns, therefore ( ( r − 1 ) / 2 p − 1 ) choices for the upward movements.
Observation 1:
As Feynman cannot move in the
−
x
or
−
y
direction, the path is guaranteed to be inside the rectangle:
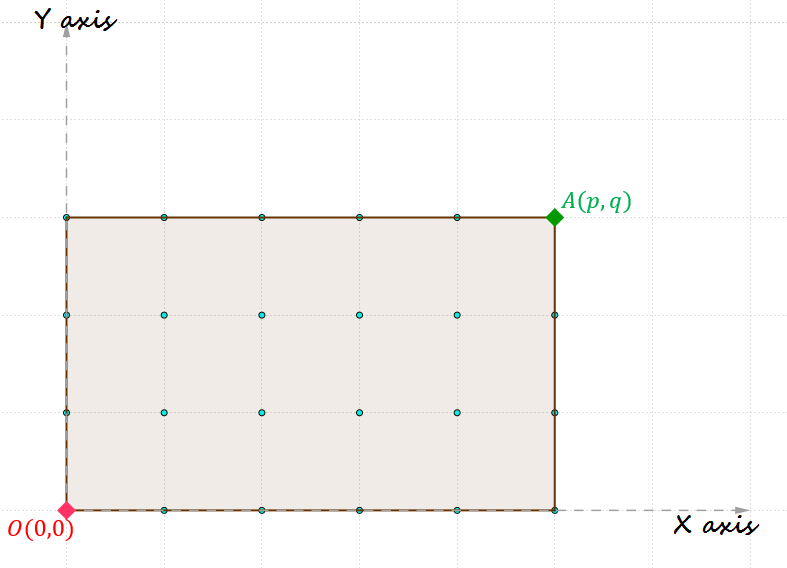
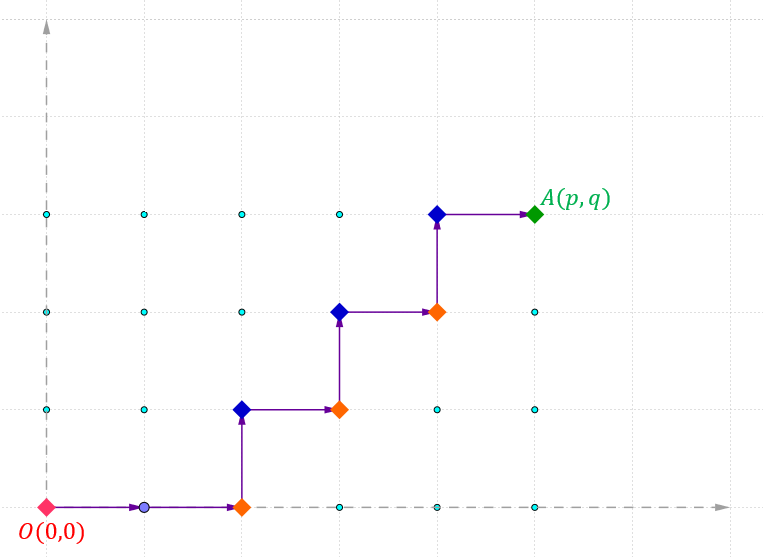
Observation 2: Suppose, Feynman starts along the x-axis.Then he makes a turn, and now he is moving along the y axis. He makes another turn and he is moving along x axis again. So it is evident that if Feynman's first step is along the x-axis, and he makes even number of turns, then his last step must be along the x-axis as well. And so on.
Observation 3:
If
r
is an even number and Feynman's first and last steps are along the x-axis, then
2
r
turns will be from x-axis to y-axis, and the other
2
r
turns will be from y-axis to x-axis. For example, there are three
x
→
y
turns (shown by orange squares) and three
y
→
x
turns (shown by blue squares) in the figure below:
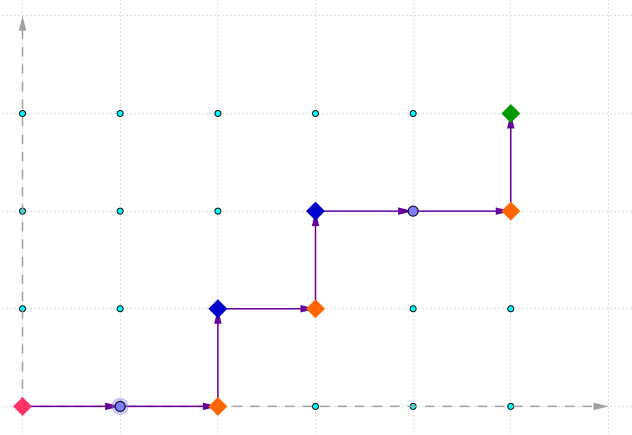
Observation 4:
If
r
is an odd number and Feynman's first and last steps are along the x-axis and y-axis respectively, then there will be
2
r
+
1
number of
x
→
y
turns, and
2
r
−
1
number of
y
→
x
turns. For example, there are three
x
→
y
turns (shown by orange squares) and two
y
→
x
turns (shown by blue squares) in the figure below:
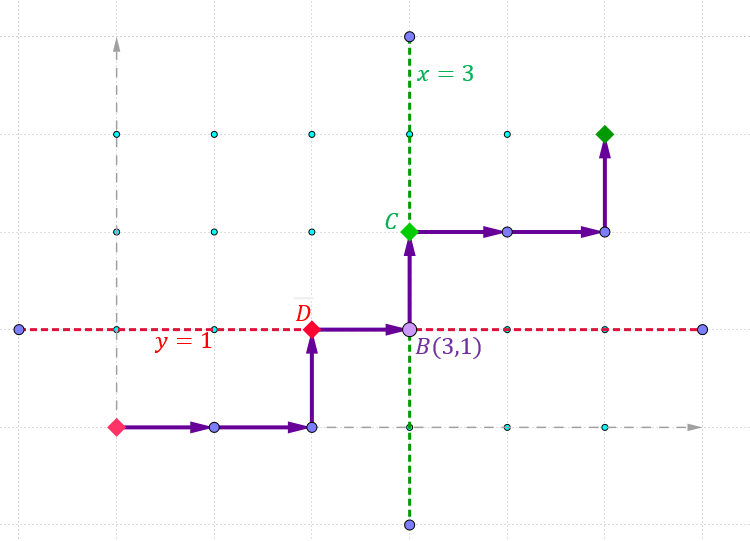
Observation 5:
Suppose Feynman makes a turn at a point
(
m
,
n
)
where
0
<
m
<
p
and
0
<
n
<
q
, then surely he makes one other turn at some point on the line
x
=
m
and yet another turn at some other point on the line
y
=
n
.
First consider the case when r is an even number:
i) Starts and ends along the x axis
There are
2
r
number of
x
→
y
turns, and
2
r
number of
y
→
x
turns. Notice, the first and last steps are along
y
=
0
and
y
=
q
lines. Surely there is a
x
→
y
turn on
y
=
0
line and a
y
→
x
turn on
y
=
q
line.
Now he chooses
2
r
lines from among the
p
−
1
vertical lines :
x
=
1
,
x
=
2
,
.
.
.
,
x
=
p
−
1
and
2
r
−
1
lines from among the
q
−
1
horizontal lines :
y
=
1
,
y
=
2
,
.
.
.
,
y
=
q
−
1
; For example, say
r
=
6
. Feynman chooses lines :
x
=
1
,
x
=
3
,
x
=
4
and
y
=
1
,
y
=
3
:
Now corresponding to this choice of lines, the path will be:
It is easy to see that there are p − 1 C 2 r ⋅ q − 1 C 2 r − 1 ways of choosing those combinations of lines.
ii) Starts and ends along the y axis
In the same way, for this case, the number of possible ways is p − 1 C 2 r − 1 ⋅ q − 1 C 2 r
Therefore, when r is even, the total number of possible ways is p − 1 C 2 r ⋅ q − 1 C 2 r − 1 + p − 1 C 2 r − 1 ⋅ q − 1 C 2 r
Now consider the case when r is an odd number: In the same procedure, it can be shown that the number of possible ways are 2 ⋅ p − 1 C 2 r − 1 ⋅ q − 1 C 2 r − 1 .
You've spent some serious time on this solution.
Truely awesome
With each step being made as either a "right" move or "up" move and knowing there are 4 steps in each direction. The route to (10,6) can be seen as a combination of independent moves along the x and y-axes.
4 steps to (0,6) has 5!/3!2! different routes and 4 steps to (10,0) has 9!/6!3! different routes
Multiply these to get 840. Then double this to reflect the starting direction along either axis.
Hi, Could you please explain the step "4 steps to (0,6) has 5!/3!2! different routes" in a bit more detail please. I follow that there must be 4 'right' and 4 'up' steps but the paths to (0,6) and 5C3 has me stumped.
Cheers Liam
Log in to reply
In this particular example it can be reached either in steps of 1,1,1,3 (4 ways) or in steps of 1,1,2,2 (6 ways).
In the more general case with m steps to reach n, it can be demonstrated inductively to be equal to (n-1)!/[(n-m)!(m-1)!]. Just consider f (n,m) = Sum f (x,m-1) for m-1 <=x <n and a familiar pattern develops.
Notice that when Feynman has to turn 7 times, he must move forward 4 times in the horizontal direction and 4 times in the vertical direction to get the destination ( 1 0 , 6 ) . Also, notice we can either start in the horizontal direction or the vertical direction, so we multiple our result by 2 when we're done. Now, we want to find the number of ways we can express 1 0 and 6 as the sum of 4 positive numbers (since each horizontal or vertical segment Feynman moves must be positive and add up to the final x or y position). So we can start listing out these ways and find the number of ways we can order the numbers. 10 1 + 1 + 1 + 7 : ( 1 4 ) = 1 ! ⋅ 3 ! 4 ! = 4 1 + 1 + 2 + 6 : ( 2 4 ) ⋅ ( 1 2 ) = 2 ! ⋅ 2 ! 4 ! ⋅ 1 ! ⋅ 1 ! 2 ! = 6 ⋅ 2 = 1 2 1 + 1 + 3 + 5 : ( 2 4 ) ⋅ ( 1 2 ) = 2 ! ⋅ 2 ! 4 ! ⋅ 1 ! ⋅ 1 ! 2 ! = 6 ⋅ 2 = 1 2 1 + 1 + 4 + 4 : ( 2 4 ) = 2 ! ⋅ 2 ! 4 ! = 6 1 + 2 + 3 + 4 : 4 ! = 2 4 1 + 2 + 2 + 5 : ( 2 4 ) ⋅ ( 1 2 ) = 2 ! ⋅ 2 ! 4 ! ⋅ 1 ! ⋅ 1 ! 2 ! = 6 ⋅ 2 = 1 2 1 + 3 + 3 + 3 : ( 1 4 ) = 1 ! ⋅ 3 ! 4 ! = 4 2 + 2 + 2 + 4 : ( 1 4 ) = 1 ! ⋅ 3 ! 4 ! = 4 2 + 2 + 3 + 3 : ( 2 4 ) = 2 ! ⋅ 2 ! 4 ! = 6 T o t a l : 4 + 1 2 + 1 2 + 6 + 2 4 + 1 2 + 4 + 4 + 6 = 8 4 6 1 + 1 + 1 + 3 : ( 1 4 ) = 1 ! ⋅ 3 ! 4 ! = 4 1 + 1 + 2 + 2 : ( 2 4 ) = 2 ! ⋅ 2 ! 4 ! = 6 T o t a l = 4 + 6 = 1 0 We can now see that there are 8 4 ways to order the horizontal segments and 1 0 ways to order the vertical segments. Now, we multiple these together (Since we must pair the horizontal combination with the vertical combination in the end) and then multiple them by 2 (We can start horizontally or vertically). 8 4 ⋅ 1 0 ⋅ 2 = 8 4 0 ⋅ 2 = 1 6 8 0
What we are looking for here is the number of sequences
(
a
1
,
b
1
,
a
2
,
b
2
,
a
3
,
b
3
,
a
4
,
b
4
)
where all terms are positive integers, and either
(i)
∑
i
a
i
=
6
and
∑
j
b
j
=
1
0
or
(ii)
∑
i
a
i
=
1
0
and
∑
j
b
j
=
6
The first type of sequence represents paths that go up first, and has four different upward paths of lengths
a
1
,
a
2
,
a
3
,
and
a
4
, respectively, and 4 different rightward paths of lengths
b
1
,
b
2
,
b
3
,
and
b
4
respectively. The sequence type of sequence represents those paths that start by going right and end by going up instead. It is clear that the number of sequences in part (i) is the same as the number of sequences in part (ii) (If not clear: map from one set to the other by moving first step to the end or vice versa).
Let
p
n
,
k
be the number of sequences of n positive integers that sum up to
k
. It is clear that the quantity we are interested in will be
2
∗
p
4
,
6
∗
p
4
,
1
0
.
Thankfully, we can express p n , k in a closed form for all n , k .
Lemma : for any value of k ≥ n , p n , k = ( n − 1 k − 1 ) To arrive at this identity, consider what we are doing when we select such a sequence. We are essentially putting k balls in n bins, but with the constraint that each bin must have at least one ball. Equivalently, we are putting ( k − n ) balls in n bins with no restrictions at all.
As others have noted, such a choice can be illustrated by a sequence of ∗ 's and ∣ 's (stars and bars), with a bar placed between collections of stars to indicate the change in bins. (For example, one way to put 5 objects in 3 bins would be ∗ ∗ ∣ ∣ ∗ ∗ ∗ .) Each sequence of stars and bars represents a different sequence, and the mapping is a complete enumeration. How many stars and bars figures are there? Note that there are ( k − n ) stars in this figure and ( n − 1 ) bars. Thus there are ( k − 1 ) total symbols of which exactly ( n − 1 ) are bars, i.e. the number of sequences is ( n − 1 k − 1 ) .
For our problem we use p 4 , 6 = ( 3 5 ) = 1 0 and p 4 , 1 0 = ( 3 9 ) = 8 4 . Summing over the parts, the total number of paths is 2 ∗ p 4 , 6 ∗ p 4 , 1 0 = 2 ∗ 1 0 ∗ 8 4 = 1 6 8 0 .
I noted that 7 turns means 8 total segments, 4 vertical and 4 horizontal. So, the total number of paths is the number of different combinations of x-values for our 4 vertical seconds, multiplied by the total possible permutations of lengths of the paths. Since we have 10 possible x-values, we have 10choose4 possible combinations of vertical bar arrangements. The rest of the path is clearly fully determined just by connecting the vertical paths by horizontal lines. For any given path, the sum of the lengths of the vertical paths must be 6. All paths least have length at least 1, and no more than 3, as to not violate the first condition for the other paths. This leaves 8 total combinations of lengths: 1113,1131,1122,1221,1211,2112,2121, and 2211. Thus, our total number of paths is 210*8=1680!
Measure the steps not from gridpoint to gridpoint, but from midpoint to midpoint ( thru the intervening gridpoint). Then each turn is a "step" of length one, half to the right and half up. The journey must begin with a half step in one direction (x or y) and end with a half step in the other direction. Ergo, rotating an x-starting path 180 degrees produces a different y-starting path. Ergo, the answer is twice the number of x-starting paths. So assume an x-starting path.
Each of the 7 turns goes up and right 1/2 step, for a total of 3 1/2 steps in each direction. The last step is a half-step up, for a total of 4 up-steps. The remaining two up-steps are placed directly following the four odd-numbered turns. There are only 10 ways to do this:
2000,0200,0020,0002,1100,1010,1001,0110,0101,0011.
Similarly, the six remaining right-steps come right before each odd-numbered turn. This one takes more counting but totals to 84: (6,0,0,0)...4 (5,1,0,0)...12 (4,2,0,0)...12 (4,1,1,0)...12 (3,3,0,0)...6 (3,2,1,0)...24 (3,1,1,1)...4 (2,2,2,0)...4 (2,2,1,1)...6
The placements of the up and right steps are independent, so the total number of x-starting paths is 10x84=840, and the overall total is twice that, 1680.
Since you can only go up or to the right, the turns must be alternating left and right turns.
Now consider that with 7 turns, there will be 4 upward movements and 4 rightward movements. We can establish a bijection between grouping upward movements and grouping stars with bars.
⋆ _ ⋆ _ ⋆ _ ⋆ _ ⋆ _ ⋆
Above, there are 6 stars, and the spaces indicate where bars can be placed to divide the stars into non-empty groups. Note that there are 5 spaces to place the bars. Since we want 4 groups, we use 3 bars. Then there are ( 3 5 ) = 1 0 ways to group the 6 stars into 4 groups. Likewise, there are 10 ways to group the 6 upward movements into 4 groups.
We can count the ways to group the rightward movements in a similar way. There are ( 3 9 ) = 8 4 ways to group the rightward movements into 4 groups.
Since these groupings are independent of each other, we can count the total number of ways to travel with 4 groups of upward movements and 4 groups of rightward movements. Note the multiplication by 2 because we can either start with an upward movement or a rightward movement:
2 ( 3 5 ) ( 3 9 ) = 2 × 1 0 × 8 4 = 1 6 8 0
In the general case of p rightward movements, q upward movements, and r turns, the number of paths is:
{ If r is even: If r is odd: ( r / 2 p − 1 ) ( r / 2 − 1 q − 1 ) + ( r / 2 − 1 p − 1 ) ( r / 2 q − 1 ) 2 ( ( r − 1 ) / 2 p − 1 ) ( ( r − 1 ) / 2 q − 1 )
In the case of r even, there aren't the same number of upward movements and rightward movements.