Feynman Long division
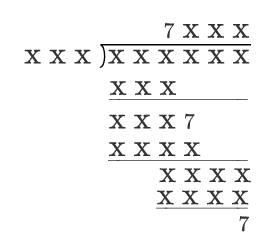
The above is a long division with most of the digits of any number hidden, except for the three 7's. Given that each of 0, 1, 2, ..., 9 was used at least once for the hidden digits, figure out all of the digits hiding and submit your answer as the value of the dividend (the 6-digit number being divided).
Details and Assumptions:
- Each represents a single-digit integer.
- The leading (leftmost) digit of a number cannot be 0.
The answer is 991750.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 7 8 0 9 1 2 7 \enclose l o n g d i v 9 9 1 7 5 0 8 8 9 0 0 0 1 0 2 7 0 0 1 0 1 6 0 0 1 1 5 0 1 1 4 3 7
Since 7 times the divisor, plus a 3 -digit number, is still a 3 -digit number, the divisor is no greater than 1 2 8 . The fourth digit of the dividend must be 7 . The third digit of the quotient must be 0 (since two digits are brought down at the last stage). Since the second and the fourth digits of the quotient multiply the divisor to give a 4 -digit number, both the second and the fourth digits of the quotient are each either 8 or 9 . Thus the quotient is one of 7 8 0 8 , 7 8 0 9 , 7 9 0 8 , 7 9 0 9 . In the first three cases (since 8 times the divisor must be a 4 -digit number), the divisor must be at least 1 2 5 . If the quotient is 7 9 0 9 , the divisor must be at least 1 1 2 .
It is now possible to check the possible divisors and quotients and, using the fact that the remainder is 7 , retrieve the possible dividends. Only three scenarios give a dividend whose fourth digit is 7 , namely 9 9 1 7 5 0 = 1 2 7 × 7 8 0 9 + 7 8 9 3 7 2 4 = 1 1 3 × 7 9 0 9 + 7 9 8 0 7 2 3 = 1 2 4 × 7 9 0 9 + 7 The second and third scenarios yield divisions which omit the digit 5 (the second omits 6 as well). On the other hand, the first scenario is just fine. From this we obtain the answer 9 9 1 7 5 0 .