$f(g(x))$ increasing, $g(f(x))$ decreasing

Here is a simple and explicit example of two such functions: First, set $f(0) = g(0) = 0$ . Define $f(x) = x$ for $x \in (1, 2]$ and $f(x) = -x$ for $x \in [-2, -1)$ . For all other $x$ , define $f$ such that $f(x) = -2f(\frac{x}{2})$ for all $x$ . $f$ looks something like this: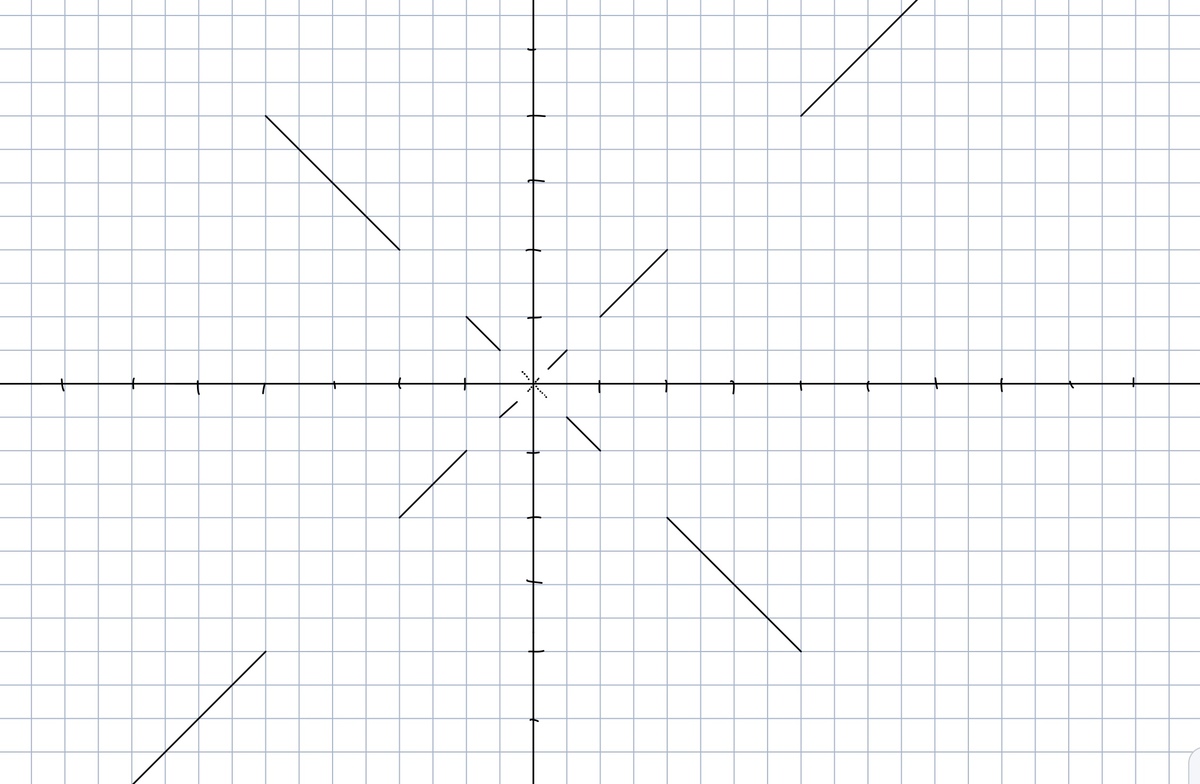

Note that $f(f(x)) = x$ , as you can check (the absolute value never changes under $f$ ). With this set up, define $g(x) = 2f(x)$ .

Now, $f(g(x)) = f(2f(x))=-2f(f(x))=-2x$ (decreasing) and $g(f(x)) = 2f(f(x)) = 2x$ (increasing).

d(f(g))/dx = df/dg * dg/dx > 0

d(g(f(x)) = dg/df * df/dx < 0

Make df/dg and dg/df negative, dg/dx negative and df/dx positive.